Recently, there has been a wave of interest in an internal notion of quantum reference frames (QRFs) [4, 5, 6] -- for example, if an interferometer has a particle travelling in a superposition of paths, "how does the particle see the interferometer" [5]? In our group, we are interested in the group-theoretic and quantum information-theoretic foundations of such QRFs, the conceptual and operational interpretation in light of a Bayesian view of the quantum state, and an axiomatic approach to formulating quantum and other physical theories relationally.
Internal perspectives and relational quantum theory
(Note: some of the following contains excerpts from our paper [1].)
All physical quantities are described relative to some frame of reference. But since all physical systems are fundamentally quantum, reference frames must ultimately be quantum systems, too. This simple insight is of fundamental importance in a variey of physical fields, including quantum information theory, quantum thermodynamics, quantum gravity, and in the foundations of quantum physics more generally.
Recently, there has been a wave of interest in a notion of "internal" QRFs, including pioneering work by Časlav Brukner's group at IQOQI [4] and several other colleagues (e.g. [5, 6, 7, 8]), but with some work dating back much earlier [9, 10]. This approach extends the usual concept of reference frames by associating them with quantum systems, and by describing the physical situation of interest from the "internal perspective" of that quantum system. For example, consider the real line R with translation symmetry, and |m> denoting the state of a quantum particle located at position m. Writing down a quantum state
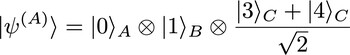
of three particles A, B, C, we can interpret it (with quite some handwaving) as expressing the quantum state "relative to A": particle A "sees itself" located in the origin, and then particle B is located at position 1, and particle C is independently located in a superposition of positions 3 and 4.
What does the situation look like "from the perspective of C"? The particle C would "locate itself" in the origin, and the description of the quantum state relative to it should read
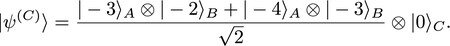
This is a state that describes A and B as entangled. Insofar as we can make sense of the idea to "jump into the perspective of one of the particles", notions of superposition and entanglement become dependent on the choice of (quantum) reference frame [4].
We can think of a QRF transformation that relates the two states. But how can we make concrete sense of the idea of "jumping into the reference frame of a particle"? How are QRF transformations different from any other unitary change of basis in a Hilbert space? What kind of physical symmetry claim is associated with the intuition that QRF changes "leave the physics invariant"?
In our group, we are interested in rigorous mathematical and information-theoretic approaches to these questions, relating these "internal" QRFs also to notions of QRFs that have been studied earlier in the context of quantum information [14, 15]. It has been shown that internal QRFs are closely related to constraint quantization [6], and thus to high energy physics, in particular to "timeless" formulations of quantum theory such as the Page-Wootters mechanism [11, 12] or the Hamiltonian constraint of loop quantum gravity [13]. We are aiming for an axiomatic approach that explores whether these constructions represent the most general way to formulate quantum theory and other physical theories relationally, or whether there are other possibilities that we have so far overlooked.
We have also studied properties of QRFs the context of quantum thermodynamics. In particular, we have shown that QRFs have to degrade on (even clever) use -- they cannot in general function as "correlating catalysts" [2].
The "paradox of the third particle"
In publication [1], we have studied internal QRFS in a special case that allows for a completely rigorous, transparent mathematical and quantum information-theoretic treatment: the case of discrete Abelian symmetry groups. We have shown that QRF transformations appear naturally as symmetry transformations of physical systems obeying a small set of conditions. In this context, important structures of constraint quantization can be shown to emerge in a very simple setting.
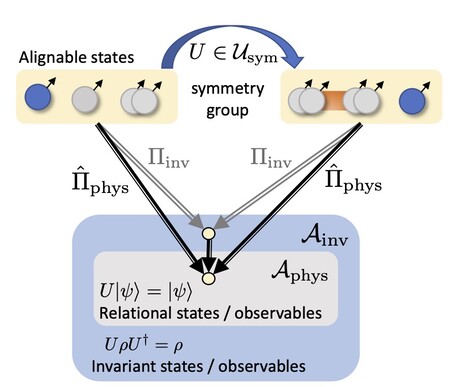
In particular, we have studied the operator-algebraic properties of observables subject to such quantum symmetries. We have analyzed how, for example, the two-particle observables can be viewed as embedded in the three-particle observables. This allowed us to resolve a puzzle from the literature known as the "paradox of the third particle" [5].
This apparent paradox can be illustrated by example of the two equations above (and the figure): how should we think of the reduced state of the two particles AC, if all QRF perspectives are physically equally correct? According to A's perspective (first equation, resp. left half of figure), the state of AC is uncorrelated with B and hence in a pure state. However, according to B's perspective (second equation, resp. right half of figure), A is entangled with B and hence AC should be in a mixed state. In other words, the answer seems to depend on how we trace out the "third particle" B.
The paradox can be resolved by acknowledging that simply computing the partial trace is the wrong thing to do in this scenario. Instead, we have to operationally define how the observables of AC are embedded in the observables of ABC, and there is essentially a unique reference-frame-independent way to do so. This leads us to a variant of the partial trace -- the relational trace -- that allows us to determine reduced states under such quantum symmetries.
In a follow-up work [3], we are currently studying how dynamics fits into this (so far, kinematical) picture.
References [our group]
[1] M. Krumm, P. A. Höhn, and M. P. Müller, Quantum reference frame transformations as symmetries and the paradox of the third particle, Quantum 5, 530 (2021). arxiv:2011.01951
[2] M. Lostaglio and M. P. Müller, Coherence and asymmetry cannot be broadcast, Phys. Rev. Lett. 123, 020403 (2019). arXiv:1812.08214
[3] P. A. Höhn, M. Krumm, and M. P. Müller, Internal quantum reference frames for finite Abelian groups, arXiv:2107.07545
References [other authors]
[4] F. Giacomini, E. Catro-Ruiz, and Č. Brukner, Quantum mechanics and the covariance of physical laws in quantum reference frames, Nat. Commun. 10, 494 (2019). arXiv:1712.07207
[5] R. M. Angelo, N. Brunner, S. Popescu, A. J. Short, and P. Skrzypczyk, Physics within a quantum reference frame, J. Phys. A: Math. Theor. 44, 145304 (2011). arXiv:1007.2292
[6] A. Vanrietvelde, P. A. Höhn, F. Giacomini, and E. Castro-Ruiz, A change of perspective: switching quantum reference frames via a perspective-neutral framework, Quantum 4, 225 (2020). arXiv:1809.00556
[7] P. A. Höhn, A. R. H. Smith, and M. P. E. Lock, The Trinity of Relational Quantum Dynamics, arXiv:1912.00033
[8] L. Loveridge, P. Busch, and T. Miyadera, Relativity of quantum states and observables, EPL 117, 40004 (2017). arXiv:1604.02836
[9] Y. Aharonov and L. Susskind, Charge Superselection Rule, Phys. Rev. 155, 1428 (1967).
[10] Y. Aharonov and T. Kaufherr, Quantum frames of reference, Phys. Rev. D 30, 368 (1984).
[11] D. N. Page and W. K. Wootters, Evolution without evolution: Dynamics described by stationary observables, Phys. Rev. D 27, 2885 (1983).
[12] W. K. Wootters, "Time" replaced by quantum correlations, Int. J. Theor. Phys. 23, 701 (1984).
[13] C. Rovelli and F. Vidotto, Covariant Loop Quantum Gravity, Cambridge University Press, Cambridge, 2015.
[14] S. D. Bartlett, T. Rudolph, and R. W. Spekkens, Reference frames, superselection rules, and quantum information, Rev. Mod. Phys. 79, 555 (2007).
[15] I. Marvian, Symmetry, Asymmetry and Quantum Information, PhD thesis, University of Waterloo, 2012.
Müller Group

Markus Müller
Group Leader+43 (1) 51581 - 9530

Manuel Mekonnen
PhD Student



