Can quantum theory be derived from simple principles, in a similar way as the Lorentz transformations can be derived from the relativity principle and the constancy of the speed of light? The exciting answer is "yes", and our group has made substantial contributions to this research goal.
Why should we "reconstruct" quantum theory?
Quantum mechanics is without doubt one of our most successful physical theories, but its textbook formulation is mysterious. Why are states of physical systems described by complex vectors in a Hilbert space? Why do observables correspond to self-adjoint operators, and why are outcome probabilities given by the Born rule?
At first sight, it may seems as if these questions are more of philosophical than of physical interest. After all, quantum theory (QT) is a mathematically well-defined, consistent framework that has successfully been applied in scientific practice for over a century. However, there are several reasons why physicists or computer scientists should be concerned with the — suitably formalized — question of “why” QT has its particular mathematical structure:
For example, motivated by the importance of experimentally testing QT, Weinberg [11] introduced a nonlinear version of QT “that can serve as a guide to experiments that would be sensitive to such [nonlinear] corrections”. Also, the problem of quantum gravity may be seen as a motivation to explore not only modifications of spacetime physics, but also of quantum physics [12]. However, finding consistent ad hoc modifications of QT turned out to be extraordinarily difficult. For example, a few months after Weinberg’s proposal of a nonlinear version of QT had appeared, Gisin [13] showed that this proposal was flawed in some sense: it allows for superluminal signalling.
Hence, simply tweaking the Hilbert space formalism of QT easily leads to undesired consequences or inconsistencies. A different strategy suggests itself: suppose that we can derive QT from a few simple, physically well-motivated postulates — operational postulates that do not directly refer to any of the mathematical machinery of QT, but only to operations that we can perform in a laboratory. For example, we can postulate that the outcome probabilities of any measurement on any given physical system are unchanged by local operations on other systems (the no-signalling principle). Once we have accomplished such a reconstruction of QT from simple postulates of this kind, there is an obvious way to obtain natural modifications of QT: drop (or weaken) one or more of the postulates, and work out what other types of theories beyond QT remain as solutions. The advantage is that these theories will be guaranteed to be consistent, and they will satisfy some important principles of QT (but not all) by construction.
There is motivation for such a strategy also beyond physics:
Are quantum computers more powerful than classical computers? It is notoriously difficult to prove the separation of complexity classes like BPP (decision problems solvable by a classical probabilistic computer in polynomial time) and BQP (its quantum analog) [14]. In order to make progress nonetheless, it has long been a strategy to consider models of computation that are not physically realizable, but that can be theoretically analyzed in ways that may ultimately shed indirect light on the difficult problems of complexity theory. The use of oracles [14] is a paradigmatic example. Contemplating computing machines in generalizations and modifications of QT [15] has already led to several interesting insights, see e.g. Refs. [16, 17, 18].
A final motivation comes simply from the desire to understand QT:
There is a paradigmatic historical example that is often cited as a role model for reconstructions of QT [19]: special relativity. Instead of simply postulating the (already known) Lorentz transformations, Einstein showed that they can be derived from essentially two simple principles: the constancy of the speed of light and the relativity principle. This was arguably an important step forward that has immensely improved our understanding of the Lorentz transformations (and of much more).
Reconstructions of QT achieve a similar goal: once one has seen such a reconstruction, the formalism becomes much less mysterious. The structure of QT, including the use of complex numbers, operators, and their algebraic structure, is demonstrated to be the unavoidable consequence of natural information-theoretic constraints. Indeed, we are already at this point: successful reconstructions of QT exist, and they arguably improve our understanding of QT quite substantially. Our research group has generated several of these reconstructions, achieving different kinds of goals and answering different kinds of questions.
Before giving an example reconstruction, let us briefly look at the history of this research area.
A brief digression into history
The idea of reconstructing QT from physically transparent principles dates back to Birkhoff and von Neumann [20]. For several decades, attempts to do so were dominated by the idea to start with the lattice of orthogonal projections (“propositions”) and their properties. This is the approach of Quantum Logic, as pursued e.g. by Mackey [21], Piron [22] and many others.
Ludwig’s axiomatization of QT, published in 1985 [23] as the culmination of decades-long work [24, 25], takes an interesting historical position. It emphasizes the notions of “states” and “effects” (formalized in terms of order unit spaces and base norm spaces) similarly as the modern formulation of Generalized Probabilistic Theories does (see below), but its derivation of Hilbert space structure is still mathematically based on the properties of the lattice of propositions (“decision effects”) as in Quantum Logic.
The immense technical complexity of Ludwig’s axiomatization, but in particular the large number of axioms illustrates what can in retrospect perhaps be regarded as one of the main weaknesses of these earlier approaches: the focus on infinite-dimensional quantum systems. While it may at first sight seem physically natural to think of quantum systems a priori as infinite-dimensional (think of the harmonic oscillator), this arguably led to works where important conceptual insights were intermingled with functional analysis technicalities in ways that made these results hard to penetrate by physicists or philosophers.
This perspective changed with the advent of quantum information theory [26]. The focus shifted twofold: first, from infinite-dimensional systems to finite-dimensional ones (“qubits”); second, from aspects of spacetime physics to compositional structure. Characteristic phenomena like entanglement, contextuality, or Bell nonlocality are all present in finite-dimensional systems, and it is those systems that represent the framework for quantum computation. The idea to build circuits from qubits, and the dramatic difference between quantum circuits and those obtained from composing classical bits, has changed the idea of what a natural axiom or principle for QT should look like.
Hence, quantum information theory can be seen as a catalyst for the next wave of axiomatizations of QT, which arguably started with Hardy’s groundbreaking work in 2001 [27]. Hardy managed to derive the Hilbert space formalism of QT from a number of “reasonable axioms”, including a simple postulate of how small systems are combined into larger ones. While Hardy’s work was a deeply inspiring and seminal result, it had one major weakness: Hardy’s reconstruction contained an axiom called “Simplicity”. In a nutshell, simplicity postulates that the simplest (smallest-dimensional) solution compatible with the other axioms is physically realized. This however left open the possibility that there is in fact an infinite sequence of theories, containing classical probability theory and QT as special cases, that satisfy the other reasonable axioms and that are hence physically as plausible as QT in some sense.
Based on Hardy’s ideas, a new surge in activity started around 2009, when three complete solutions to the reconstruction problem appeared at almost the same time [1, 28, 29]. Our contribution [1] was one of them, summarized below. Before describing it, we have to set the stage by defining the general framework in which we formulate our postulates.
General Probabilistic Theories
In order the reconstruct QT from simple principles, we need a mathematical framework in which the principles can be formulated. This framework should be based on absolutely minimal assumptions — essentially, it should contain only structural elements that represent self-evident features of general laboratory situations. It should admit a large class of theories, with QT as just one possible theory among many others.
The framework of Generalized Probabilistic Theories (GPTs) satisfies all these desiderata. A thorough, mathematically rigorous, yet pedagogical introduction to GPTs can be found in my “Les Houches lecture notes” [2]; other introductions (though with slightly different formalism) can be found in Refs. [16, 27], for example. Here, I will only give a very sketchy and incomplete overview.
The paradigmatic laboratory situation considered in the GPT framework is the one sketched in the figure below: the preparation of a physical system is followed by a transformation and, finally, by a measurement that yields one of several possible outcomes with some well-defined probability.
The results of the preparation procedure are described by states, and the set of all possible states in which a given system can be prepared is its state space. Every possible state space defines a GPT system, up to a single constraint: we would like to be able to "toss a coin" and prepare one of two given states at random, with a certain probability. This introduces a notion of affine-linear combinations on the state space, which (together with a notion of normalization) implies that state spaces are convex subsets of some vector space over the real numbers.
Transformations map states to states, and they must be consistent with the preparation of statistical mixtures, i.e. they must be linear maps. Outcome probabilities are described by linear functionals ("effects") on the space of states. And this is essentially all that is assumed.
Two special cases are of particular importance:
- Quantum theory (QT). Systems are characterized by an integer n (the maximal number of perfectly distinguishable states), and the states are the (n × n) density matrices. The transformations are the completely positive, trace-preserving maps, and the effects are given by positive semidefinite operators with eigenvalues between 0 and 1 (POVM elements).
Among the transformations, the reversible transformations (those that can be undone) are the unitary maps. - Classical probability theory (CPT). For given n, the state are the n-outcome probability vectors. The transformations are the channels, i.e. stochastic matrices, and effects are given by non-negative vectors. The reversible transformations are the permutations of the configurations.
In addition to QT and CPT, there is a continuum of GPTs with different kinds of physical properties. For example, a GPT called "boxworld" contains states that violate Bell inequalities by more than any quantum state [16]. Other GPTs predict interference of "higher order" than QT [30], a prediction that can in principle be tested experimentally [31]. Note that typical GPT do not carry any kind of algebraic structure -- there is in general no notion of "multiplication of observables".
The "landscape" of GPTs provides a simple and extremely general framework in which QT can be situated. The goal of a reconstruction is then to provide a set of principles, or postulates, that single out QT as the unique GPT that satisfies these principles.
Quantum theory from three principles
In Ref. [1], we prove that QT (as defined above) is the unique probabilistic theory that satisfies the following three principles:
- Tomographic Locality: States of composite systems AB are uniquely characterized be the statistics and correlations of local measurements on A and on B.
- Subspace Axiom: Consider a system with n perfectly distinguishable states. The subset of states for which the n-th outcome has probability zero is equivalent to a system with (n-1) perfectly distinguishable states.
- Continuous Reversibility: For every pair of pure states, there is a one-parameter group of reversible transformations that maps one to the other.
Note that these postulates are operational and not formal: they refer to operations that we can perform in a laboratory, and to statistical properties of outcomes that we observe. For example, a "pure state" is defined as a state of maximal knowledge, i.e. a state that cannot be prepared by tossing a coin and preparing one of two distinct states at random. In particular, this does not assume that pure states are vectors in a Hilbert space. The postulates make sense in every GPT, and do not refer to the specific mathematical framework of QT. In particular, the fact that states are operators on a complex Hilbert space is derived, not assumed.
These three principles have already been introduced by Hardy [27], who however did not prove that they imply QT (Hardy had to supplement them with additional assumptions). Note that we make two background assumptions that are arguably part of the choice of framework: first, the assumption that the state spaces are finite-dimensional (which is natural because we are only concerned with systems with a finite number n of perfectly distinguishable states); second, the assumption that the sets of effects and states are full duals of each other (the "no-restriction hypothesis" [32, 33]), i.e. that every valid probability assignment on the states can in principle describe the outcomes of a conceivable measurement.
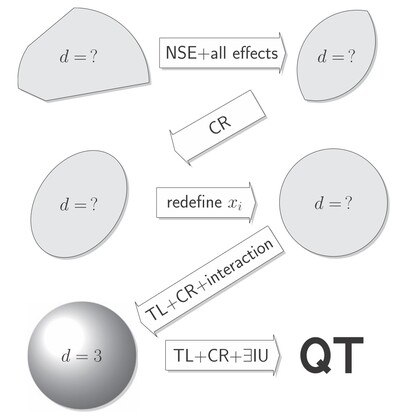
This figure sketched part of the proof strategy (it is taken from another publication [3] and the labelling is not exactly fitting, but the overall strategy is the same). For the details, see our paper [1] or the Les Houches lecture notes [2]. We start by considering a generalized bit in a GPT that satisfies our postulates, i.e. a system with n=2 distinguishable states. A priori, its state space could be described by any convex set of any dimension d (top left). However, the subspace axiom gives us some information about two-outcome measurements. Working out the consequences, we find that the state space must be strictly convex: it cannot contain any lines in its boundary (top right).
Next, the postulate of Continuous Reversibility enforces a strong notion of symmetry on the state space: due to group representation theory, it implies that the state space must be the unit ball of an invariant inner product (middle left), which we can reparametrize to correspond to a Euclidean unit ball (middle right). We have thus "almost" arrived at the Bloch ball, which is known to describe the quantum bit. However, at this point, we do not yet know that the Bloch ball must be three-dimensional, i.e. we do not know the value of d.
This is only shown in a next step, by considering two generalized bits. The subspace axiom and tomographic locality imply certain consistency conditions on how any logical bit can be embedded into two bits, which finally implies that d=3: we have derived the dimension of the Bloch ball! Some additional non-trivial arguments are needed to show that a collection of n generalized bits must be equivalent to the state space of n quantum bits, and then known theorems about quantum computation tell us that the reversible transformations must correspond to conjugations with unitaries.
Further contributions from our group
Over the last few years, we have contributed to the reconstruction program in a variety of ways. In a number of publications, we have in particular pursued the following goals:
- Derive QT from even fewer or weaker assumptions [3, 4, 5, 6]. This is an obvious kind of improvement of the reconstruction results that aims at distilling the "ultimate essence" of QT into a few simple principles.
- Give a reconstruction of QT with principles that only talk about single systems [7]. Such a reconstruction is particularly promising for finding "QT's closest cousins": theories that appear as solutions if we drop or weaken some of the postulates that are known to imply QT. This strategy is extremely difficult to pursue for postulates that talk about composite systems, because composition implies a large variety of consistency conditions that have to be upheld. In contrast, it is much simpler to give examples of single systems that satisfy some, but not all principles of QT.
- Show that some elements of QT are necessary consequences of other things we know about physics. For example, some elements of QT can be understood as unavoidable consequences of consistency with thermodynamics as we know it [8]. Strong self-duality (between states and measurements) of QT is a consequence of "bit symmetry" [9]. Furthermore, the dimensionality of the Bloch ball can be derived from relativity of simultaneity on an interferometer [10] (for details, see "General Probabilistic Theories"). This suggests that the structures of QT and of spacetime mutually constrain each other (see also "Black boxes in space and time"), which yields a fascinating insight into the logical architecure of our world.
Other recent results
A lot of progress and insights have been gained since the appearance of the first full reconstructions. For example, there is now a new reconstruction by Hardy [34] which does not make use of the Simplicity Axion, a diagrammatic reconstruction based on category theory [35], a reconstruction “from questions”, i.e. based on the complementarity structure of propositions [36, 37]; there are several beautiful works by Wilce on deriving the more general Jordan-algebraic state spaces from the existence of “conjugate systems” resembling QT’s maximally entangled states (e.g. [38]). Barnum and Hilgert have proven an immensely deep result that improves our reconstruction of QT from single-system postulates [39]. This list is far from complete, and it certainly excludes important work that does not fall into the GPT framework but relies, for example, more on the device-independent formalism (as sketched briefy in "Black boxes in space and time").
References [our group]
[1] Ll. Masanes and M. P. Müller, A derivation of quantum theory from physical requirements, New J. Phys. 13, 063001 (2011). arXiv:1004.1483
[2] M. P. Müller, Probabilistic Theories and Reconstructions of Quantum Theory (Les Houches 2019 lecture notes), SciPost Phys. Lect. Notes 28 (2021). arXiv:2011.01286
[3] Ll. Masanes, M. P. Müller, R. Augusiak, and D. Pérez-García, Existence of an information unit as a postulate of quantum theory, Proc. Natl. Acad. Sci. USA 110(41), 16373 (2013). arXiv:1208.0493
[4] Ll. Masanes, M. P. Müller, R. Augusiak, and D. Pérez-García, Entanglement and the three-dimensionality of the Bloch ball, J. Math. Phys. 55, 122203 (2014). arXiv:1111.4060
[5] G. de la Torre, Ll. Masanes, A. J. Short, and M. P. Müller, Deriving quantum theory from its local structure and reversibility, Phys. Rev. Lett. 109, 090403 (2012). arXiv:1110.5482
[6] M. Krumm and M. P. Müller, Quantum computation is the unique reversible circuit model for which bits are balls, npj Quantum Inf. 5. 7 (2019). arXiv:1804.05736
[7] H. Barnum, M. P. Müller, and C. Ududec, Higher-order interference and single-system postulates characterizing quantum theory, New J. Phys. 16, 123029 (2014). arXiv:1403.4147
[8] M. Krumm, H. Barnum, J. Barrett, and M. P. Müller, Thermodynamics and the structure of quantum theory, New J. Phys. 19, 043025 (2017). arXiv:1608.04461
[9] M. P. Müller and C. Ududec, Structure of reversible computation determines the self-duality of quantum theory, Phys. Rev. Lett. 108, 130401 (2012). arXiv:1110.3516
[10] A. J. P. Garner, M. P. Müller, and O. C. O. Dahlsten, The complex and quaternionic quantum bit from relativity of simultaneity on an interferometer, Proc. R. Soc. A 473, 20170596 (2017). arXiv:1412.7112
References [other authors]
[11] S. Weinberg, Testing Quantum Mechanics, Ann. Phys. (NY) 194, 336--386 (1989).
[12] O. Oreshkov, F. Costa, and Č. Brukner, Quantum correlations with no causal order, Nat. Commun. 3, 1092 (2012).
[13] N. Gisin, Weinberg's non-linear quantum mechanics and supraluminal communications, Phys. Lett. A 143, 1 (1990).
[14] S. Aaronson, Quantum computing since Democritus, Cambridge University Press, New York, 2013.
[15] D. S. Abrams and S. Lloyd, Nonlinear quantum mechanics implies polynomial-time solution for NP-complete and sharp-P problems, Phys. Rev. Lett. 81, 3992 (1998).
[16] J. Barrett, Information processing in gneeralized probabilistic theories, Phys. Rev. A 75, 032304 (2015).
[17] C. M. Lee and J. Barrett, Computation in generalised probabilistic theories, New J. Phys. 17, 083001 (2015).
[18] J. Barrett, N. de Beaudrap, M. J. Hoban, and C. M. Lee, The computational landscape of general physical theories, npj Quantum Inf. 5, 41 (2019).
[19] R. Clifton, J. Bub, and H. Halvorson, Characterizing Quantum Theory in Terms of Information-Theoretic Constraints, Found. Phys. 33(11), 1561 (2003).
[20] G. Birkhoff and J. von Neumann, The logic of quantum mechanics, Ann. Math. 37, 823 (1936).
[21] G. Mackey, Mathematical Foundations of Quantum Mechanics, W. A. Benjamin, New York, 1963.
[22] C. Piron, Axiomatique Quantique, Helv. Phys. Acta 37, 439 (1964).
[23] G. Ludwig, An Axiomatic Basis for Quantum Mechanics. Volume 1: Derivation of Hilbert Space Structure, Springer, Berlin, 1985.
[24] G. Ludwig, Die Grundlagen der Quantenmechanik, Springer, Berlin Heidelberg, 1954.
[25] G. Ludwig, Versuch einer axiomatischen Grundlegung der Quantenmechanik und allgemeinerer phsyikalischer Theorien, Z. Phys. 181, 233--260 (1964).
[26] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 2000.
[27] L. Hardy, Quantum Theory From Five Reasonable Axioms, arXiv:quant-ph/0101012.
[28] B. Dakić and Č. Brukner, Quantum Theory and beyond: Is entanglement special?, in “Deep Beauty. Understanding the Quantum World through Mathematical Innovation”, edited by H. Halvorson (Cambridge University Press, New York, 2011). arXiv:0911.0695
[29] G. Chiribella, G. M. D’Ariano, and P. Perinotti, Informational derivation of quantum theory, Phys. Rev. A 84, 012311 (2011). arXiv:1011.6451
[30] R. D. Sorkin, Quantum Mechanics as Quantum Measure Theory, Mod. Phys. Lett A 9, 3119 (1994). arXiv:gr-qc/9401003
[31] U. Sinha, C. Couteau, T. Jennewein, R. Laflamme, and G. Weihs, Ruling Out Multi-Order Interference in Quantum Mechanics, Science 329, 418 (2010). arXiv:1007.4193
[32] G. Chiribella, G. M. D'Ariano, and P. Perinotti, Probabilistic theories with purification, Phys. Rev. A 81, 062348 (2010).
[33] P. Janotta and R. Lal, Generalized probabilistic theories without the no-restriction hypothesis, Phys. Rev. A 87, 052131 (2013).
[34] L. Hardy, Reformulating and reconstructing quantum theory. arXiv:1104.2066.
[35] J. H. Selby, C. M. Scandolo, and B. Coecke, Reconstructing quantum theory fro diagrammatic postulates, Quantum 5. 445 (2021). arXiv:1802.00367
[36] P. A. Höhn, Toolbox for reconstructing quantum theory from rules on information acquisition, Quantum 1, 38 (2017).
[37] P. A. Höhn and A. Wever, Quantum theory from questions, Phys. Rev. A 95, 012102 (2017).
[38] A. Wilce, A Royal Road to Quantum Theory (or Thereabouts). arXiv:1606.09306
[39] H. Barnum and J. Hilgert, Strongly symmetric spectral convex bodies are Jordan algebra state spaces. arXiv:1904.03753