Caslav Brukner
- Scientific & Deputy Executive Director
- Group Leader
- +43 (1) 4277 - 72582
- Caslav.Brukner(at)oeaw.ac.at
Quantum mechanics (QM) is our most successful physical theory ever in terms of experimental prediction, and yet the interpretations of its formalism still give rise to a number of open problems. Among those, the quantum measurement problem is one of the most fundamental and its supposed solutions lay at the core of the controversy over the alternative interpretations of quantum theory. The measurement problem can be thought of as the problem of how, when and under what circumstances definite values of physical variables are obtained, namely what distinguishes a measurement from the standard (i.e. unitary) evolution in QM.
The measurement problem has gained renewed interest in recent years due to novel, extended versions of the famous Wigner’s friend (gedanken) experiment (such as the much debated Frauchiger-Renner no-go theorem on the self-consistency of quantum theory). Wigner’s friend-like scenarios comprise observations of observers, highlighting the ambiguity of the two dynamics of quantum theory: Unitary evolution of isolated quantum systems and the non-unitary measurement-update rule (or collapse postulate). These (thought) experiments are designed such that the regular observers – Friends – would describe their interaction with another quantum system as a measurement and, therefore, apply the collapse postulate, while so-called superobservers – Wigners – describe the Friends as quantum systems and, thus their interactions unitarily.
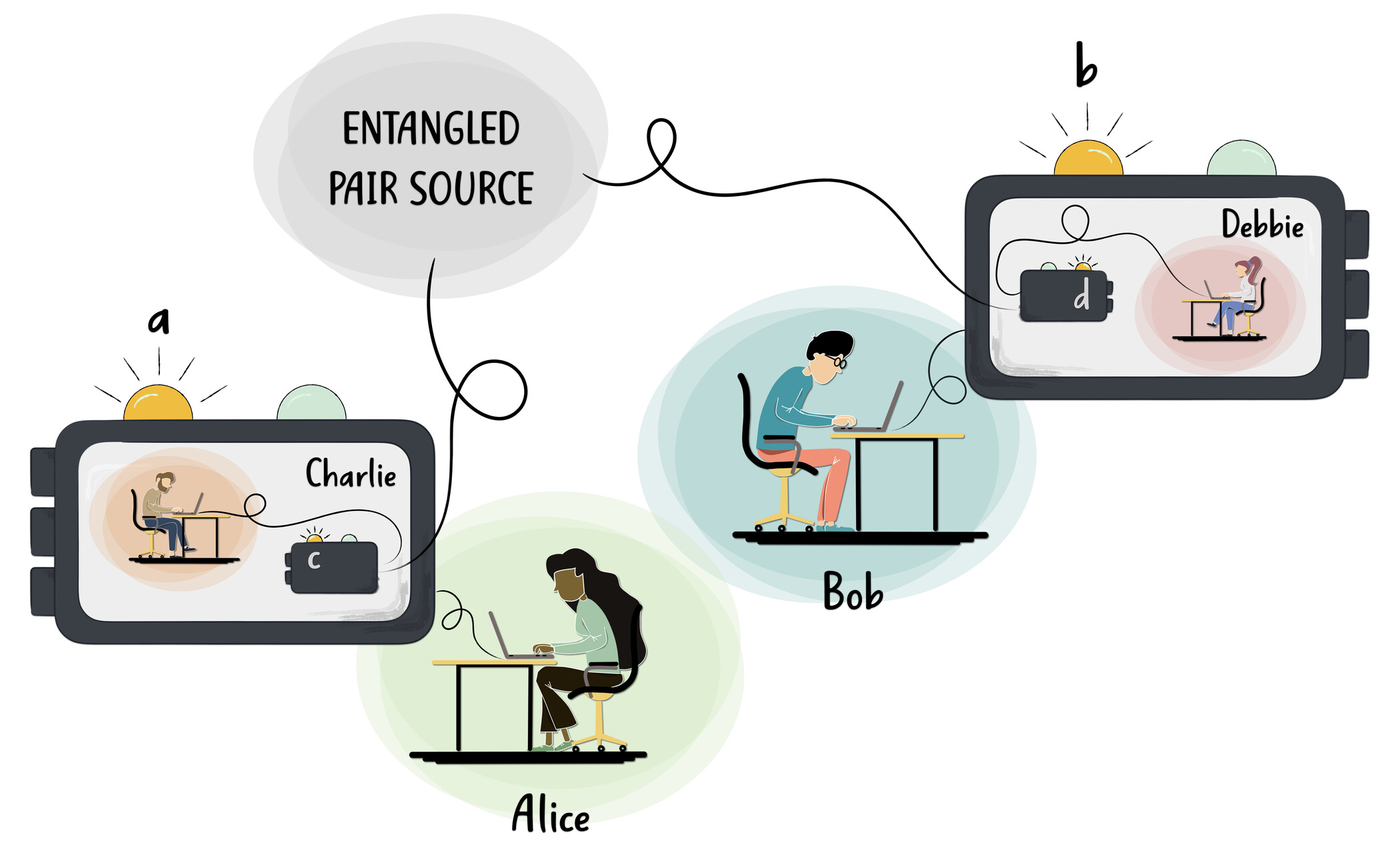
Since 2015, our group works towards a better understanding of the measurement problem, by exploring the limits of applicability of quantum theory in exotic scenarios in which observers both perform measurements and are measured by superobservers. We were the first ones to derive a no-go theorem for “facts of the world”, based on a combination of Winger’s friend with Bell-like setups [1], and we further developed there ideas in [2-4].
The no-go theorem demonstrates that there cannot be a generally valid theory (possibly beyond QM) in which Wigner’s and Wigner’s friend’ facts can jointly be considered as (local) objective properties. More precisely, it shows that the assumptions on “locality”, “freedom of choice” and the assumption of observer-independent facts (i.e. where one can simultaneously decide on the truth value of statements about the experimental outcomes observed by different observers) are incompatible with quantum mechanical predictions. This has even stronger implications than standard Bell’s theorem, since it excludes the possibility of a coexistence of outcomes for different observers: “there are no facts of the world per se, but only relative to observers” [1] (given all the other assumptions hold). The empirical content of our argument, i.e. the violation of a Wigner-Bell inequality, has been confirmed [5], although with a very minimal observer model that allowed for considering photons as Friends. Moreover, its theoretical basis has been strengthened and further experimental confirmations carried out [6].
Moreover, we showed that different dynamical descriptions of the same measurement, together with the standard probability rules, give rise to observable contradictions when certain classical records are exchanged between Wigner and the Friend [7]. We thus focused on generalizing the standard Born rule, such that to reconcile the two different probability assignments in the descriptions by Wigner and his friend. This was achieved by describing the Wigner’s friend experiment in a timeless framework (Page-Wootters mechanism) which allows to assign an overall state from which both Wigner and the Friend can unambiguously compute the probabilities. While this resolves the ambiguity between the application of unitary dynamics and state-update rule (“collapse”), we found that there are at least three different ways to assign probabilities, all of which resolve the Wigner’s friend paradox in different ways [8]. Finding compelling physical arguments to single out one rule among probability assignments would significantly contribute to solving the Wigner’s friend paradox and thus bringing new insight on the quantum measurement problem.
[1] C. Brukner, On the quantum measurement problem, Quantum [Un]-Speakables II. Springer International Publishing, 95-117 (2017).
[2] C. Brukner, A no-go theorem for observer-independent facts. Entropy 20, 5 (2018).
[3] V. Baumann, F. D. Santo, and C. Brukner, Comment on Healey's \Quantum Theory and
the Limits of Objectivity, Foundations of Physics 49, 741 (2019).
[4] V. Baumann and S. Wolf, On Formalisms and Interpretations, Quantum2 (2018).
[5] M. Proietti, A. Pickston, F. Graffitti, P. Barrow, D. Kundys, C. Branciard, M. Ringbauer and A. Fedrizzi, Experimental test of local observer independence, Science Advances 5, 9 (2019).
[6] K.W. Bong, A. Utreras-Alarcón, F. Ghafari, Y.C. Liang, N. Tischler, E.G. Cavalcanti, G.J. Pryde and H.M. Wiseman, Testing the reality of Wigner's friend's experience, arXiv preprint arXiv:1907.05607 (2019).
[7] V. Baumann and C. Brukner, Wigner’s Friend as a Rational Agent, Chapter in “Quantum, Probability, Logic”, Springer (2020).
[8] V. Baumann, F. Del Santo, A.R.H. Smith, F. Giacomini, E. Ruiz-Castro and C. Brukner, Generalized probability rules from a timeless formulation of Wigner's friend scenarios. preprint arXiv:1911.09696, 2019.
[9] K. Bong, A. Utreras-Alarcón, F. Ghafari, et al. A strong no-go theorem on the Wigner’s friend paradox, Nat. Phys. (2020).
This video lecture by Časlav Brukner on the topic.