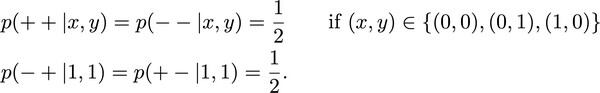We thank the Austrian Science Fund (FWF) for support (P 33730-N). Click here for the project's description on the FWF website.
Popular summary -- scientific details below:
Quantum theory has not only revolutionized our understanding of physics, but it has also led to a multitude of technological applications in information theory. For example, quantum physics admits unconditionally secure cryptography or the generation of provably random numbers. In black box quantum information theory, this approach is taken one step further: security of cryptography or randomness can be guaranteed even if the devices involved in the protocol are untrusted (device-independence), or even if the validity of quantum theory itself is not taken for granted. In this setting, security follows solely from the observed statistics of the devices (seen as black boxes) and from simple physical principles, without any further assumptions.
Previous research has focused on black boxes with abstract inputs and outputs, such as abstract bits (zeros and ones) as commonly used in information theory. But in many actual experiments, the inputs and outputs are not abstract, but concrete spatiotemporal quantities like the spatial direction of a magnetic field, the duration of a pulse, or the angle of a polarizer. The goal of this project is to theoretically analyze the foundations and applications of such spatiotemporal black boxes.
On the one hand, we hope that this analysis will give us fundamental insights into the relation between quantum theory, space and time: how do the statistical predictions of quantum theory fit into space and time? For example, do spatiotemporal symmetries constrain the probabilities of detector clicks, or the correlations between distant events, even without assuming the validity of quantum theory? What can we conclude with certainty if we build an experiment, set up temporal pulses or spatial fields, and then measure a certain statistics? Can we construct fundamentally new tests of quantum theory in this setting? On the other hand, we will explore how these insights can be put to use in quantum information theory, in particular in the context of semi-device-independent protocols. The security of such protocols is often based on abstract assumptions about the involved quantum systems, such as upper bounds on the information content of the transmitted systems. One goal of this research is to replace such abstract assumptions by more concrete, physically better motivated suppositions, in particular assumptions about the interplay of the systems with space and time. Furthermore, we hope to obtain new methods to detect the presence of so-called Bell nonlocality in realistic quantum systems.
Black boxes: on device-independent quantum information
Quantum cryptography and the generation of random numbers are two important applications of quantum information theory (QIT). Ideally, we would like to base the security of such protocols on as few assumptions as possible. Device-independent [7,8,9] and semi-device-independent [10,11,13] protocols offer a kind of "gold standard" towards this goal. For example, there are protocols that allow two parties (say, Alice and Bob) to establish a provably secure cryptographic key if only two assumptions are satisfied:
- the no-signalling principle: there is no instantaneous information transfer between Alice and Bob;
- a violation of a Bell inequality [12].
In principle, we can guarantee that there is no signalling by placing Alice and Bob at spacelike separation, such that special relativity forbids information transfer on the relevant time scales. The violation of a Bell inequality is a statistical phenomenon that Alice and Bob can observe in their recorded data. No assumptions on the devices have to be made (they could have been bought from the eavesdropper) - we do not even have to assume the validity of quantum theory! In principle, all components of the experiment are modelled as "black boxes" [12]: unknown physical systems with some specific observable statistical input-output behavior. It is remarkable that such black-box descriptions are sufficient to guarantee the functionality and security of some quantum information-theoretic protocols.
In addition to these applications, this black-box picture has proven immensely useful for the study of the foundations of quantum physics. For example, we can ask about the set of correlations that any physical theory admits in a causal scenario as the one in the figure above. What possible probability tables p(a,b|x,y) (also called "behaviors" or "correlations") can we generate? Bell's theorem [12] tells us that there exist correlations that can be obtained within quantum physics in this scenario, but not within classical physics, as certified by the violation of a Bell inequality. For example, correlations that arise from certain measurements on a singlet state have this property. Despite these difference, classical and quantum correlations satisfy one common constraint. These are the no-signalling conditions [12]: Bob's choice of input y ("choice of measurement") has no impact on the marginal probabilities of Alice's outcome a, and vice versa:
In a relativistic universe, these conditions are crucial: if they were violated, we could construct a "Bell telephone" that allows us to transmit information faster than light. This is impossible in classical and quantum physics. However, quantum physics does not give us the most general correlations that satisfy the no-signalling constraints: there are conceivable correlations that are non-signalling, but that violate Bell inequalities by more than any quantum state. An example is given by "Popescu-Rohrlich" ("PR-box") [10] correlations: Alice and Bob both choose a single bit as input, i.e. x,y∈{0,1}, and they each obtain either +1 or -1 as outputs, i.e. a,b∈{-1,+1}. The PR-box probabilities are
That is, the outcomes are either perfectly anticorrelated (if Alice and Bob choose inputs "1") or otherwise perfectly correlated. This probability table satisfies the no-signalling conditions, but it cannot be realized in a Bell scenario within quantum physics, since it would violate the so-called Tsirelson bound for the Bell-CHSH scenario.
The situation can be illustrated as follows:
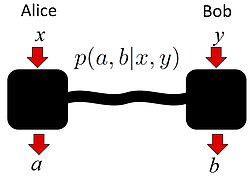
The set of classical correlations C is a strict subset of the set of quantum correlations Q, which in turn is a strict subset of the set of non-signalling correlations NS. Both C and NS are polytopes (for any fixed number of parties, inputs and outputs), but Q is not. The set of quantum correlations Q sits strangely "in between" the most restrictive (classical) and most general (non-signalling) possibilities. "Why" does nature admit the set of correlations Q, and not a smaller or larger set? Instead of simply postulating the validity of quantum theory, can we perhaps find physical principles that determine Q? The last few years have seen tremendous research efforts on this question, and some fascinating partial results, but the general problem is still open (see, however, the other research area "Reconstructions of Quantum Theory" where the analogous task has indeed been achieved).
Our research project builds on these previous findings, but studies one additional and surprisingly insightful aspect: the role of space and time.
Putting the black boxes into space and time
Within this project, our group is reconsidering the "black-box" approach - not only for Bell scenarios as sketched above, but also for more general settings, such as semi-device-independent prepare-and-measure scenarios. As we have seen above, the inputs and outputs of black boxes are typically considered to be abstract labels, for example single bits. However, in many (if not all) experimentally relevant scenarios, the inputs are spatiotemporal quantities: for example, directions of a magnetic field, the duration of a pulse, or the the angle of a polarizer.
In other words, inputs and/or outputs of the black boxes are often quantities that break a spatiotemporal symmetry: physical systems that carry group representations. Do these symmetries impose additional constraints on the correlations? Do they yield additional information that can play a similar role as the (ultimately spatiotemporally motivated) no-signalling principle - perhaps information that we can use as well-motivated assumptions in semi-device-independent scenarios? These are some of the questions that we address in our project. Our aim is two-fold:
- To analyze how the structures of spacetime and quantum theory mutually constrain each other. This is a foundational question motivated by pure curiosity, where we aim for insights into the logical structure of the physical world.
- To use the additional structures and constraints, via group representation theory, to construct novel device- or semi-device-independent protocols, or to identify "metrological games" in which quantum theory can be compared to other theories.
In our work [1], we have introduced the general framework of "spacetime boxes", and we have proven a few first results, including an exact characterization of the quantum (2,2,2)-Bell correlations.
Exact characterization of the (2,2,2)-quantum correlations
Consider a Bell scenario where Alice and Bob each obtain one of two possible outcomes, a,b∈{-1,+1}, and each of them can choose between two possible inputs. However, now we assume that Alice and Bob reside in d-dimensional space (where d≥2), and that their inputs are spatial directions: unit vectors on which they can act with the rotation group SO(d). For example, we could have d=3, and the choice of inputs could be given by setting a magnetic field (or its inhomogeneity) in a specific direction. Now we make one specific assumption and a non-assumption:
- We do not assume that quantum theory holds. That is, we base our proofs and calculations only on probability theory, and we demand that the probabilities respond to rotations in a consistent way.
- We assume that "the probabilities transform locally like vectors". This physics jargon means mathematically that the rotations RA, RB that Alice and Bob perform locally to choose their inputs act locally via the fundamental (and/or trivial) representation of SO(3).
In our paper [1], we prove that these conditions uniquely characterize the set of quantum correlations Q as depicted in the figure above -- in the special case of (2,2,2)-correlations, i.e. if we have 2 parties (Alice and Bob), each having a choice of 2 inputs and obtaining one of 2 possible outputs:
Theorem. Every correlation that can be obtained under these two assumptions is a quantum correlation, i.e. can be realized within quantum theory. Furthermore, all (2,2,2)-quantum correlations can be realized under these two assumptions (restricting Alice and Bob to two possible input directions) if we supplement Alice and Bob with shared randomness.
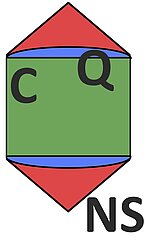
For example, consider the case d=2 depicted above. In this case, the input (unit vectors) can be parametrized by single angles. We can think of Alice (and Bob) choosing her (his) input by rotating a polarizer by a certain angle α (resp. β), obtaining outcome +1 if the particle passes the polarizer and -1 otherwise, yielding correlations p(a,b|α,β), The set of probability tables that can be realized in this scenario, assuming that the probabilities "transform like vectors" as described above, that Alice and Bob are restricted to two possible choices of angles, and that Alice and Bob have a supply of shared randomness, is exactly the set Q of (2,2,2)-quantum Bell correlations.
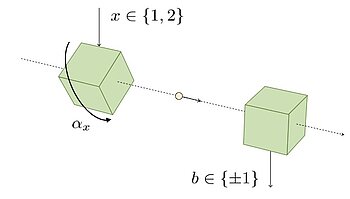
A theory-independent randomness generator
In our paper [5], we have shown how the ideas above can be used to construct a semi-device-independent randomness generator whose security does not rely on the validity of quantum theory. Consider a prepare-and-measure scenario as depicted in the figure. The preparation device accepts an input x (which is either 1 or 2): if the input is 1, then nothing happens; if the input is 2, then the preparation box is rotated by some fixed angle α around a fixed axis (for example, around the beam axis). Then the box prepares a physical system (for example, a quantum particle) and sends it to the measurement device, which in turn produces an output b (either +1 or -1).
The goal of this scenario is to certify that the outcome b is random: no agent can completely predict this outcome, even if they hold an arbitrary amount of additional information that even we, the constructors of the experiment, might lack (say, about the detailed composition or movement of molecules at the boxes). Denoting this additional information by λ, we would like, for example, the conditional entropy H(B|X,Λ) to be non-zero (and, ideally, to be large). This would allow us to extract a number of random bits from our measurement results that are provably unpredictable by any eavesdropper (as long as they hold no quantum side information).
This is impossible, however, without making some assumptions on the system that is being sent to the measurement device. For semi-device-independent scenarios like this, a standard assumption is to bound the Hilbert space dimension of the transmitted quantum system (for example, assuming that these systems are qubits), see e.g. [13]. However, this is arguably not a particularly physically well-motivated assumption. Here, we replace it by a physically more meaningful one: we upper-bound the total spin of the transmitted physical system. This is an assumption that can be formulated within quantum theory, but also beyond it: it means that the outcome probabilities P(b|x=2,λ) are trigonometric polynomials of degree at most 2J in the angle α. For example, if the spin is upper-bounded by J=1, then
P(b|x=2,λ) = c0 + c1 cos α + s1 sin α + c2 cos(2α) + s2 sin(2α)
for every λ, where the ci and si are suitable real constants that depend on b and λ. That the rotation group is represented with spin at most J=1 is provably equivalent to obtaining this form (and more generally for other J). But the condition via trigonometric polynomials makes sense without assuming quantum theory (and it follows, indeed, from representations of the rotation group on more general state spaces). That is, instead of assuming something about the Hilbert space dimension, we are assuming something about the way that the transmitted system reacts to spatial rotations. We can think of this as a "rotation box": a black box that responds to spatial rotations somehow (and as described further below, this strictly generalizes the possible quantum behaviors).
In [5], we have now proven the following surprising fact: the set of correlations that quantum theory predicts (derived in [13]) for this setup is exactly identical to the set of correlations achievable in this more general rotation box scenario. As a consequence, the security of the randomness generation protocol, and the number of extractable random bits, is the same regardless of whether we assume quantum theory or not. In other words: the relevant predictions of quantum theory can be derived without assuming quantum theory, merely from the structure of space.
Rotation boxes and metrological games
How can physical systems respond to spatial rotations, in any physical theory? In [6], we have given a thorough mathematical analysis of this question in terms of "rotation boxes", which are analogous to the well-known notion of non-local boxes. We have proven that quantum theory admits the most general rotational correlations for spins 0, 1/2, and 1, but we describe a metrological game where beyond-quantum resources of spin 3/2 outperform all quantum resources of the same spin.
We have proven a multitude of fundamental results about those correlations, including an exact convex characterization of the spin-1 correlations, a Tsirelson-type inequality for spins 3/2 and higher, and a proof that the general spin-J correlations admit an efficient outer SDP approximation to the quantum set. Our results illuminate the foundational question of how space constrains the structure of quantum theory, they build a bridge between semi-device-independent quantum information and spacetime physics, and they demonstrate interesting relations to topics such as entanglement witnesses, spectrahedra, and orbitopes.
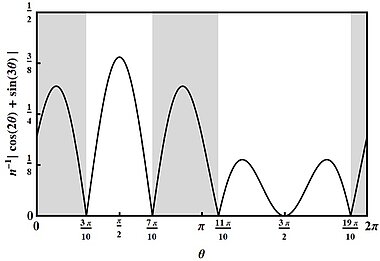
The metrological game that we consider is sketched in upper figure: a physical system of spin at most 3/2 undergoes an unknown rotation by some angle θ, and the task is to estimate some function of θ by measuring the system on some clever way. In this case, the goal is not to determine an accurate estimate of θ (as in usual metrological tasks), but to ask whether θ is in some range of angles depicted in gray in Figure 2 below. (The a priori probability of lying in the gray or white region is 1/2 each.) Moreover, θ has not been chosen uniformly at random, but according to the probability distribution that is depicted in the lower figure.
It turns out that quantum spin-3/2 systems allow us to win this game with a probability of 85.4%, whereas there are more general beyond-quantum spin-3/2 systems (described by rotation boxes) that allow us to win the game with the maximal probability of 88.3%. Moreover, this gap does not appear for spins 0, 1/2, or 1 -- and proving this latter statement ist mathematically pretty difficult, involving an exact convex characterization of the set of spin-1 correlations.
Further topics
We are exploring a range of further topics, such as relating spacetime boxes to self-testing, making folklore "entanglement from conservation laws" arguments device-independent, or finding functionals on symmetry groups that cannot be extended to larger groups. If you have any further questions, feel free to contact us.
References (our group)
[1] A. J. P. Garner, M. Krumm, and M. P. Müller, Semi-device-independent information processing with spatiotemporal degrees of freedom, Phys. Rev. Research 2, 013112 (2020). arXiv:1907.09274
[2] A. J. P. Garner, M. P. Müller, and O. C. O. Dahlsten, The complex and quaternionic quantum bit from relativity of simultaneity on an interferometer, Proc. R. Soc. A 473, 20170596 (2017). arXiv:1412.7112
[3] P. A. Höhn and M. P. Müller, An operational approach to spacetime symmetries: Lorentz transformations from quantum communication, New J. Phys. 18, 063026 (2016); in NJP's "Highlights of 2016" collection. arXiv:1412.8462
[4] M. P. Müller and Ll. Masanes, Three-dimensionality of space and the quantum bit: an information-theoretic approach, New J. Phys. 15, 053040 (2013); in NJP's "Highlights of 2013" collection. arXiv:1206.0630
[5] C. L. Jones, S. L. Ludescher, A. Aloy, and M. P. Müller, Theory-independent randomness generation with spacetime symmetries. arXiv:2210.14811.
[6] A. Aloy, T. D. Galley, C. L. Jones, S. L. Ludescher, and M. P. Müller, Spin-bounded correlations: rotation boxes within and beyond quantum theory, arXiv:2312.09278.
References (other authors)
[7] A. Acín, N. Brunner, N. Gisin, S. Massar, S. Pironio, and V. Scarani, Device-Independent Security of Quantum Cryptography against Collective Attacks, Phys. Rev. Lett. 98, 230501 (2007). arXiv:quant-ph/0702152
[8] J. Barrett, L. Hardy, and A. Kent, No Signaling and Quantum Key Distribution, Phys. Rev. Lett. 95, 010503 (2005). arXiv:quant-ph/0405101
[9] R. Colbeck, Quantum And Relativistic Protocols For Secure Multi-Party Computation, PhD thesis, University of Cambridge, 2006. arXiv:0911.3814
[10] M. Pawłowski and N. Brunner, Semi-device-independent security of one-way quantum key distribution, Phys. Rev. A 84, 010302(R) (2011). arXiv:1103.4105
[11] H. Li, Z. Yin, Y. Wu, X. Zou, S. Wang, W. Chen, G. Guo, and Z. Han, Semi-device-independent random-number expansion without entanglement, Phys. Rev. A 84, 034301 (2011). arXiv:1108.1480
[12] N. Brunner, D. Cavalcanti, S. Pironio, V. Scarani, and S. Wehner, Bell nonlocality, Rev. Mod. Phys. 86, 419 (2014). arXiv:1303.2849
[13] T. van Himbeeck, E. Woodhead, N. J. Cerf, R. García-Patrón, and S. Pironio, Semi-device-independent framework based on natural physical assumptions, Quantum 1, 33 (2017).