If you ask a particle physicist or a cosmologist what they think about quantum physics, they will tell you that this theory has passed all experimental tests. Therefore, the universe is undoubtedly quantum.
They are wrong.
Due to the high cost of describing many-body quantum states, extracting predictions from quantum physics is typically impossible. If we used all the computers in the world to carry out numerical simulations, we would be stuck with quantum systems of around 60 particles or less.
So when people say: “quantum physics has passed all the tests”, what they actually mean is that quantum physics has passed all the tests in all situations where we are able to make a prediction. Those are not that many situations: essentially, the spectra of small molecules, the behavior of light and the outcomes of experiments where a few elementary particles interact.
This is the actual experimental status of quantum physics. Everything else is wishful thinking.
To say that “because we haven’t found any contradiction so far, quantum physics must be the ultimate theory” reveals a poor knowledge of the history of science. 150 years ago, all experiments performed by humankind were compatible with Newtonian mechanics. Until 19th century chemists started exploring the spectrum of hydrogen and found an anomaly that they couldn’t explain.
With quantum physics, it will be the same. One day, someone somewhere will conduct an experiment that cannot be described by any quantum theory. It is just a matter of time.
To this, there are two possible attitudes: we can sit and wait for this experiment to come… or we can actively search for clues of non-quantumness.
The limits of quantum theory
In the device-independent approach to quantum theory, introduced by Popescu and Rohrlich, experiments are viewed as black boxes which admit a classical input (say, the type of experiment conducted) and return a classical output (the experimental result). No assumptions are made on the inner mechanisms that led to the generation of the experimental result: in this framework, the only information we can hope to gather from several repetitions of sequential or simultaneous experiments is the probability distribution of the outputs conditioned on the inputs.
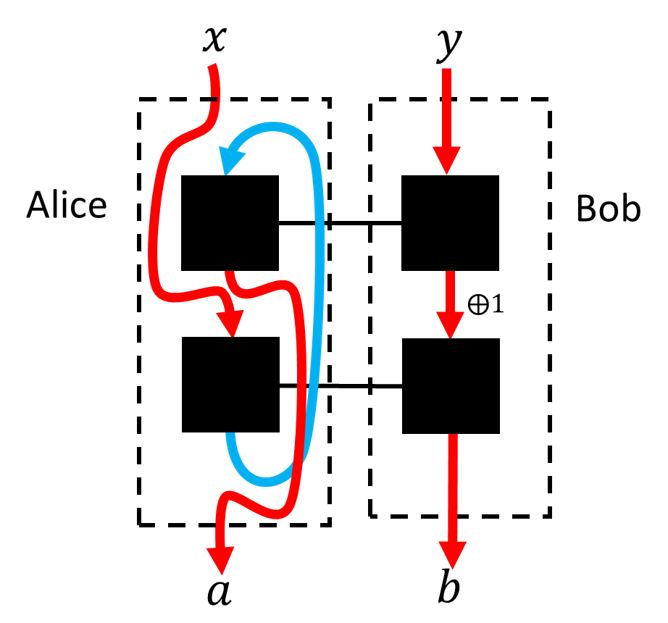
The figure bellow shows, for instance, how to model a bipartite experiment within the black-box formalism. Alice (Bob) inputs a symbol x (y) in her (his) lab, obtaining output a (b ). By conducting several repetitions of this experiment, they manage to estimate the probabilities P(a,b|x,y) .
The advantage of this black box description of reality is that it is theory-independent. The framework does not make any assumption about the underlying physical theory describing the experiment, other than that it must predict the measurement statistics P(a,b|x,y) . The framework does not posit, e.g., that Alice and Bob are measuring the polarization of a bipartite optical system, be it classical, quantum or else.
John S. Bell famously used the black box framework to devise a quantum experiment to refute classical physics. Intuitively, there exist distributions P(a,b|x,y) , achievable in certain quantum experiments, that nonetheless do not admit a classical realization. These distributions are said to be Bell non-local (or, simply, non-local). They have been observed in quantum optics experiments, thus falsifying classical physics.
As observed by Tsirelson, the black box framework is wide enough to accommodate the possibility that the contents of the box might not follow the laws of quantum mechanics. For instance, any Bell experiment satisfying
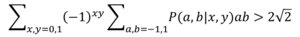
would disprove the universal validity of quantum mechanics.
In general, proving that no bipartite quantum state and local quantum measurement operators can give rise to the observed statistics P(a,b|x,y) is a difficult mathematical problem, as such impossibility statements must hold over all Hilbert spaces, finite or infinite dimensional, where such a bipartite quantum state might act. In fact, the problem of deciding whetherPa,bx,y is close to a quantum realizable distribution is logically undecidable.
In 2006, we proposed a hierarchy of efficiently computable outer approximations to the set of quantum correlations to tackle this problem [1]. The Navascués-Pironio-Acín (NPA) hierarchy is essentially the only systematic procedure to disprove the existence of a quantum model in a device-independent test. Not surprisingly, it quickly found application in device-independent quantum information science. It also marked the birth of Non-Commutative Polynomial Optimization theory [2].
Further modifications of the NPA hierarchy can be used to bound Alice’s and Bob’s Hilbert space dimension [3, 4] or make claims about the quantum state contained in the box and the quantum measurements effected by the two parties [5, 6]. This procedure, known as self-testing, is based on the fact that certain correlations P(a,b|x,y) only admit a unique quantum representation.
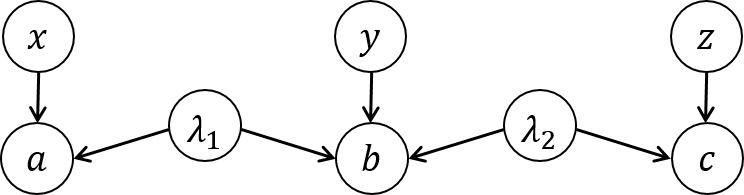
By generalizing the notion of a Bell experiment, we can identify further experimental scenarios to test quantum theory. In this direction, note that bipartite Bell scenarios can be regarded as a particular class of causal structures, see the figure below.

In the picture, λ represents the bipartite state shared by Alice and Bob; and the variables x and y , Alice and Bob’s measurement settings. The variables a and b are respectively influenced by λ and x and λ and y . Note that, while x,y,a,b are all observed variables, λ is hidden, and can just be indirectly accessed through a,b .
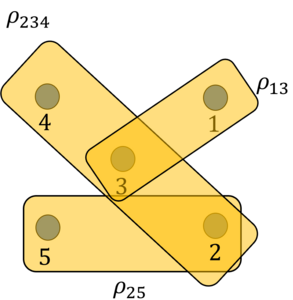
Beside Bell scenarios, there exist more complicated causal structures, such as the 3-in-line scenario, depicted below.
In this scenario, two bipartite state sources, λ1, λ2 influence the observed variables a, b, c according to the arrows. This causal scenario is different from a tripartite Bell experiment, where a single hidden source λ would be influencing the three variables a, b, c simultaneously. As we will soon see, the experimental realization of general causal structures allows one to separate the correlations of distinct physical theories that would be otherwise indistinguishable in standard Bell scenarios. Moreover, one such experiment might bring in the future a disproof of the universal validity of quantum theory.
As in the Bell scenario, proving that a given distribution is not quantum realizable within a given causal structure is an arduous task. In fact, even deciding whether a distribution of observed variables is classical-realizable is a challenging mathematical problem. So challenging, indeed, that it is famous: in the field of causal inference, it is known as the causal compatibility problem. In 2016 a team of physicists at Perimeter Institute conceived a hierarchy of linear programming relaxations of the set of classical-realizable correlations for each conceivable causal structure. This hierarchy was dubbed theinflation technique.
In collaboration with one of the creators of the method, we proved in [9] that the inflation technique is complete, i.e., that any distribution of observed variables that cannot be realizable within the considered causal structure must necessarily violate one of the conditions of the inflation hierarchy. We moreover proved that any distribution of observable variables passing the nth inflation test must be O(n) -close to a classical realizable distribution. The 30-year old causal compatibility problem had been solved… by physicists!
In [8] we generalize the inflation technique to tackle the analog quantum problem. In this case, though, the conditions of quantum inflation do not suffice to characterize quantum-realizable correlations. In fact, due to the undecidability of characterizing bipartite quantum nonlocality, we know that no algorithmic hierarchy can possibly suffice. Empirically, we nonetheless observe that quantum inflation allows computing very good relaxations to quantum limits that couldn’t be calculated otherwise. If any such relaxation were violated in experiment, we would have disproven quantum theory.
The following example will illustrate the power of causal network experiments to falsify reasonable physical theories. Real quantum mechanics (RQM) is the result of restricting all states, operators and maps in standard quantum physics to have real, as opposed to complex, entries. In this seminal paper it was proven that RQM and standard quantum mechanics predict the same set of probability distributions in Bell experiments, no matter the number of separate parties. The common perception among the quantum foundations community was therefore that RQM was physically equivalent to standard quantum mechanics: any quantum mechanical experiment could be explained within the framework of RQM.
In [9] we however show that quantum experiments in the 3-in-line scenario can generate correlations that RQM cannot approximate arbitrarily well. This means that, in principle, one can conduct a quantum experiment to falsify RQM. The experiment we proposed required distributing two maximally entangled two-qubit states between the separate parties Alice and Bob and Bob and Charlie, see the figure below.
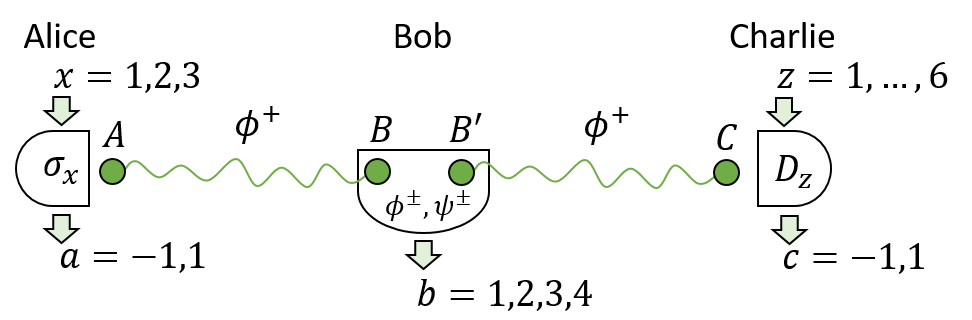
In our proposed experiment, Alice can measure her qubit with either of the three Pauli matrices, that is, x=1,2,3 . Bob has no measurement settings (alternative, we can think that his setting y can only take one value); he is required to conduct a full Bell-state measurement, which will project Alice and Bob’s state to a maximally entangled state. For any pair of Alice’s measurements, Charlie will choose a pair of directions in the Bloch sphere that guarantee that he and Alice can maximally violate the Clauser-Horn-Shimony-Holt inequality. Charlie must hence conduct one of 6 possible dichotomic measurements.
As shown in [9], the measurement statistics P(a,b,c|x,z) so obtained (a list of 288 probabilities) cannot be approximated arbitrarily well if the two distributed states and all measurement operators are required to have real entries. This is so even if we allow the four local Hilbert spaces involved (A,B,B’,C in the figure) to be infinite dimensional. To arrive at this result, we build on previous works on self-testing and on a dynamical interpretation of the NPA hierarchy.
Recent experimental implementations of our proposal have confirmed the predictions of standard quantum theory, thereby ruling out the universal validity of RQM.
The other worlds
Leaving aside the titanic task of falsifying quantum theory, suppose, that, in effect, quantum theory were not fundamental. What kind of correlations P(a,b|x,y) could we expect to observe in a post-quantum world? This question was the starting point of an ambitious research program that started in 1992, with the work of Popescu and Rorhlich. In their paper, the two authors observed that the principle of no-superluminal signalling did not suffice to enforce quantum correlations (note, however, that Tsirelson noted this mismatch a few years before). Following Popescu and Rohrlich’s paper, there was a flurry of results that tried to bound the nonlocality of any supraquantum theory through reasonable physical principles. The principles put forward had colorful names, like Non-trivial Communication Complexity, No Advantage for Nonlocal Computation, Information Causality, and Local Orthogonality.
In this direction, we proposed the principle of Macroscopic Locality [10]. In a nutshell, this axiom demands that coarse-grained extensive measurements of natural macroscopic systems must admit a classical description.
Consider a standard experiment of bipartite nonlocality, conducted by two parties, Alice and Bob, as shown below

A pair of particles is generated, Alice and Bob subject them to interactions x, y and, finally, they impinge on detectors a, b with probability P(a,b|x,y) . In a macroscopic version of this experiment, N pairs of particles are created, Alice and Bob interact with each particle beam in ways x,y , and different intensities are measured in each detector.

When the number of pairs tends to infinity, it can be shown that, if the particles follow the laws of quantum physics, the resulting probability density ρ(I1,…,J1,…|x,y) can be explained by classical Physics. That is, two macroscopic observers would not need to invoke non-classical theories to make sense of their experiments. In contrast, when the beam is composed of particle pairs described by certain supraquantum distributions, such as the Popescu-Rohrlich box, the macroscopic observations ρ(I1,…,J1,…|x,y) defy the laws of classical physics. Macroscopic Locality demands the existence of a classical limit for this class of experiments, and hence the PR-box is not supposed to appear in any reasonable physical theory.
The set of microscopic bipartite boxes P(a,b|x,y) satisfying Macroscopic Locality is slightly bigger than the quantum set. Hence, as far as ML goes, there is room for physical theories beyond quantum mechanics. This set is also the first non-trivial example of a set of correlations closed under wirings.
By wirings, or combining inputs and outputs of independent boxes, one can generate a new effective box, see the figure below.
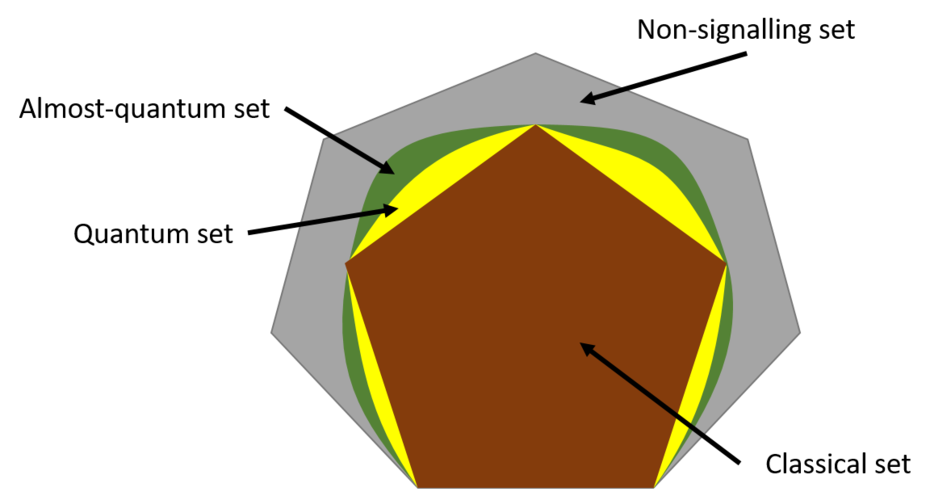
Clearly, if the original boxes can be realized in a given physical theory, so can the final effective box. In other words: physical sets of boxes must be closed under wirings. The condition of being closed under wirings limits severely the geometry of the physical sets. For years, only a handful of closed sets were identified: the classical set, the quantum set, the set of boxes compatible with macroscopic locality and the set of boxes compatible with relativistic causality (also known as the non-signalling set). These sets had a “Russian-doll” structure, i.e., the classical set is contained in the quantum set, that is contained in the Macroscopic Locality set, that is contained in the non-signalling set. The evidence therefore pointed that the framework of black boxes could only accommodate finitely many different physical theories and that those formed a hierarchy.
In [11] we showed that, on the contrary, there exist infinitely many sets closed under wirings. Moreover, some of them satisfy non-trivial inclusion relations.
As explained in [11], the last result implies that there exist information-theoretic physical principles which are unstable under composition. For any such principle Q , there exists a pair of boxes P1,P2 such that infinitely many copies of one or the other are compatible with Q , but no physical theory can contain both P1 andP2 while satisfying Q . Therefore expressions such as “the set of all correlations satisfying the principle of Information Causality”, widely used in foundations of physics, may not have any meaning at all. It is interesting to remark that Macroscopic Locality can be shown not to exhibit this pathology: any number of boxes satisfying Macroscopic Locality cannot be engineered to violate this physical principle.
Long after the discovery of the afore-mentioned physical principles, it was still not clear whether any of these or a subset of them was strong enough to single out quantum nonlocality. This would have implied that, at least at the level of correlations, there exist no reasonable physical theories beyond quantum physics.
This state of affairs changed in 2014, when we identified a supra-quantum set of correlations that, with the possible exception of Information Causality, does not violate any of the aforementioned principles [12] (there is plenty of numerical evidence that suggests that it also satisfies Information Causality). We call it the almost quantum set. It emerges naturally in a consistent histories approach to theories beyond quantum mechanics, and, contrary to the quantum set, whose characterization we know to be undecidable, it admits a computationally efficient description.
At the time, we conjectured that the almost quantum set corresponds to the set of correlations of a yet-to-be-discovered consistent physical theory; similar to quantum mechanics, albeit arguably more plausible.
Nowadays, we are not so optimistic: in [13] we show that almost quantum correlations do not emerge from any physical theory satisfying the No-Restriction Hypothesis (NRH). The NRH essentially demands that any mathematically well-defined measurement must admit a physical realization. In a sense, the NRH captures the spirit of the scientific method: we test the validity of scientific theories by making predictions beyond the framework where they are known to be successful. E.g.: from Einstein’s equations we predicted the existence of black holes long before we had any observational evidence. Alternatively, we could have modified the theory of General Relativity to forbid the existence of such unobserved objects.
This is not the end of the story, because the NRH seems to be unfalsifiable through Bell or Bell-type experiments. This puts into question the physicality of the NRH, rather than that of the almost quantum set.
The Limits of Many-Body Quantum Systems
Many-body systems offer an essentially virgin landscape to test the limits of quantum theory. The lack of control in manipulating these systems, together with the astronomical numbers of subsystems involved, make full state tomography an impossible task. Hence, the assumption of an underlying quantum state for the whole system is more a matter of faith than a testable physical prediction.
The hope to falsify the validity of quantum mechanics in many-body systems naturally leads to the quantum marginal problem: given the near-neighbor density matrices of a solid state system, does there exist a global density matrix that admits the former as marginals?
The resolution of the quantum marginal problem in the negative would imply the inability of quantum theory to make sense of the considered many-body experiment.
Unfortunately, the quantum marginal problem is known to be Quantum-Merlin-Arthur-hard, so it is unlikely that an efficient (let alone analytic!) general solution exists. This does not mean, however, that one cannot solve it at all: for all we know, there could exist an algorithm that solves most instances of the problem.
To solve the quantum marginal problem in the negative, it suffices to formulate a tractable relaxation (i.e., a superset) of the set of near-neighbor reduced density matrices of many-body quantum systems: if the experimental data lies outside the relaxation, then it is incompatible with a global quantum state. Some relaxations of the set of quantum marginals have been proposed (see, e.g., this paper and this paper), all of them quite loose.
In [14] we use notions from statistical physics to tackle the quantum marginal problem. Essentially, we show that, to each quantum renormalization flow, there corresponds a relaxation of the set of quantum marginals. This nicely complements the observation by Verstraete and Cirac that every class of renormalization flows can be turned into an ansatz (subset) of many-body states: the so-called tensor network states.
Our correspondence works like this: each renormalization transformation connects two weak relaxations of different coarse-grained versions of the original many-body system. This leads to a tower of convex optimization constraints, whose height corresponds to the flow length: taken together, these constraints provide a non-trivial, tractable relaxation of the set of quantum marginals.
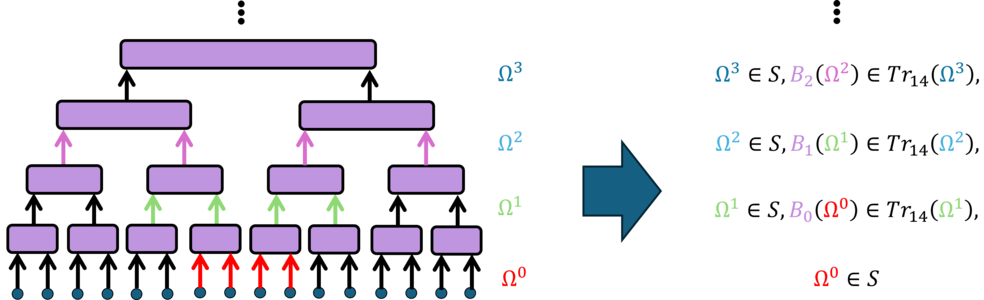
By varying the renormalization scheme, we tighten this relaxation in different regions of the set of reduced density matrices. Thus, tailoring the renormalization flow to the input of the marginal problem, we can solve the latter in cases where all other numerical methods fail.
How does this method work in practice? In [14] we use it to estimate the minimum energy density of translation-invariant quantum systems. Note that, while the Verstraete-Cirac correspondence leads to a numerical method to upper bound ground state energies, our correspondence allows lower bounding ground state energies. We observe that, in 1D translation-invariant quantum systems, both methods typically return very similar numbers, see the figure below.
[1] M. Navascués, S. Pironio and A. Acín, Bounding the set of quantum correlations, Phys. Rev. Lett. 98, 010401 (2007).
[2] M. Navascués, S. Pironio and A. Acín, Noncommutative Polynomial Optimization. Handbook onSemidefinite, Cone and Polynomial Optimization, M.F. Anjos and J. Lasserre (eds); Springer, 2011.
[3] M. Navascués and T. Vértesi, Bounding the set of finite-dimensional quantum correlations, Phys. Rev. Lett. 115, 020501 (2015).
[4] M. Navascués, A. Feix, M. Araújo and T. Vértesi, Characterizing finite-dimensional quantum behavior, Phys. Rev. A 92, 042117 (2015).
[5] T. H. Yang, T. Vértesi, J.-D. Bancal, V. Scarani and M. Navascués, Robust and versatile black-box certification of quantum devices, Phys. Rev. Lett. 113, 040401 (2014).
[6] J.-D. Bancal, M. Navascués, V. Scarani, T. Vértesi and T. H. Yang, Physical characterization of quantum devices from nonlocal correlations, Phys. Rev. A 91, 022115 (2015).
[7] M. Navascués and E. Wolfe, The Inflation Technique Completely Solves the Causal Compatibility Problem, Journal of Causal Inference 8(1) (2020).
[8] E. Wolfe, A. Pozas-Kerstjens, M. Grinberg, D. Rosset, A. Acín and M. Navascués, Quantum Inflation: A General Approach to Quantum Causal Compatibility, Phys. Rev. X 11, 021043 (2021).
[9] M.-O. Renou, D. Trillo, M. Weilenmann, T. P. Le, A. Tavakoli, N. Gisin, A. Acín and M. Navascués, Quantum physics needs complex numbers, arXiv:2101.10873.
[10] M. Navascués and H. Wunderlich, A glance beyond the quantum model, Proc. Royal Soc. A 466:881-890 (2009).
[11] B. Lang, T. Vértesi and M. Navascués, Closed sets of correlations: answers from the zoo, Journal of Physics A 47, 424029 (2014).
[12] M. Navascués, Y. Guryanova, M. J. Hoban, A. Acín, Almost quantum correlations, Nat. Comm. 6, 6288 (2015).
[13] A. B. Sainz, Y. Guryanova, A. Acín and Miguel Navascués, Almost quantum correlations violate the no-restriction hypothesis, Phys. Rev. Lett. 120, 200402 (2018).
[14] Kull, N. Schuch, B. Dive and M. Navascués, Lower Bounding Ground-State Energies of Local Hamiltonians Through the Renormalization Group, arXiv:2212.03014 (accepted in Phys. Rev. X).