If Time is really only a fourth dimension of Space, why is it, and why has it always been, regarded as something different? And why cannot we move in Time as we move about in the other dimensions of Space?

H.G. Wells, The Time Machine.

The notion of time translation, the possibility to make an object (or subject) age faster than usual, or even reverse its natural dynamics, is as old as civilization. It features in Indian texts from year 400 B.C., and was the subject of theological discussions during the Middle Ages in Europe. In [1, 2] we investigate this question from the point of view of non-relativistic quantum theory. We find that one can engineer particle beams with a very surprising property: they make any quantum system they scatter with leap backwards in time!

In quantum theory, the dynamics of any closed system are governed by a Hamiltonian or energy operator H . Left alone, a quantum system originally in state |ψ〉  will evolve according to the Schrödinger equation:

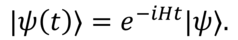
The system will experience a non-trivial time translation when, after a time T’ , its final state is e-iHT|ψ〉  rather than e-iHT'|ψ〉 , with T different fromT' . If T>T’>0  (T’>T>0 ), we say that the system has been fast-forwarded (time-dilated); if T<0 , the system has been rewound.

Our investigation in [1,2] revolves around the notion of a universal time-translation process (UTTP). Such is a physical process with the property that any target quantum system where it acts will experience a specific time translation. Crucially, this must be so independently of how each of the steps of the process affects the target. Note that the same physical operation can cause different systems to react in different ways. For example, turning on a magnetic field (the operation) will cause the spins of a muon, an electron and a neutron to evolve differently, since they have different magnetic moments. A UTTP should, however, induce the same time translation on these three systems. This last feature, universality, is what sets our work apart from other attempts to control the dynamics of a quantum system.

UTTPs, if they exist, must be probabilistic, since there is always the chance that our actions do not affect the target system at all (in which case, the probability of success is zero). We nonetheless require that the success of the process be heralded: that is, at some point the process must output whether the desired time translation took place or not.

Even allowing for probabilistic implementations, one can easily show that, if there is no information whatsoever about the target system, then universal time translation is impossible. Hence, in [1, 2] we assume that the Hilbert space dimension of the target is known.

To recap, a universal time translation process is a sequence of physical operations together with a measurement that, applied to any target quantum system of a given dimension, will time-translate the system in a non-trivial way, independently of how the target system reacts to each individual operation.

In [1, 2] we find that the only possible UTTPs are those that time-translate a d -dimensional target system in time T’  by an amount T∈ [-T’/(d-1), T’] . Fast-forwarding is thus impossible, but one can nonetheless rewind a quantum system by some amount. All such protocols can be realized through a scattering experiment, see the figure below.

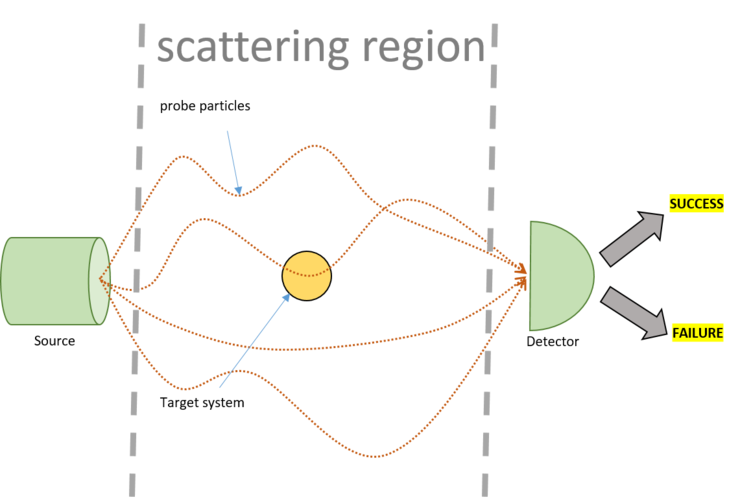
Sketch of a time translation experiment. The probe particles are produced in a controlled lab (the source) and then released to the scattering region, where the target system lies. Upon leaving the scattering region, the scattered particles are subject to a quantum measurement, the outcome of which shows whether the target was indeed time-translated.

In this experimental setup, the target system is placed in a scattering region, where, if left undisturbed, will evolve through its free (unknown) Hamiltonian H . To interact with the target, we prepare probes in a controlled lab, make them scatter against the target and measure them afterwards. The outcome of this measurement indicates whether the time translation process was successful.

While in the scattering region, the probes will interact with the target according to unknown time-independent Hamiltonian interactions that by assumption we cannot control. The only elements under our control in the scattering experiment are how we prepare the probes (namely, in which quantum state), when we release them and how we measure them. As it turns out, for every dimension d  there exists a prepare-and-measure protocol with the property that, independently of the interactions between the d -dimensional target and the probes, guarantees that the former be time-translated by the desired amount T .

In [2] we also study UTTPs acting on several identical systems, i.e., systems with the same free and interaction Hamiltonians (but in principle different states). In that case, we can consider processes that time-translate each individual system by a different amount of time. We find that, while one still cannot fast-forward all systems at once, one can relocate at will evolution time from one system to another. This allows us to devise scattering experiments that, acting on n  systems for time T’ , propagate one of them nT’ time units to the future, while keeping the rest in the same state they were at the beginning of the experiment. We call this phenomenon universal time transfer.

The above are not just theoretical fantasies: in fact, the simplest UTTPs have already been used to rewind a photon’s polarization and a superconducting qubit. As predicted by the theory, by the end of either experiment, the observed final state of the target was the same that the system had some time before the UTTP began.

As we already explained, UTTPs cannot be deterministic. In case of an unsuccessful realization, it is, however, possible to run a further scattering protocol that, if successful, will undo the effect of the previous protocol on the targets and time-translate the latter as originally desired [1]. It is not clear if, through concatenation of several such correction steps, one can always increase the overall probability of success arbitrarily (except for a subset of probe-target interactions of measure zero). In [3] we nonetheless present one such protocol, which rewinds two-level systems with an arbitrarily high probability of success. The problem of generalizing this result to higher dimensional targets remains open.

[1] M. Navascués, Resetting uncontrolled quantum systems, Physical Review X 8, 031008 (2018).

[2] D. Trillo, B. Dive and M. Navascués, Translating uncontrolled systems in time, Quantum 4, 374 (2020).

[3] To appear.

Navascués Group