Current experimental devices built by Google and IBM have recently demonstrated control over quantum systems composed of hundreds of qubits. Certifying that any such enormously complex system possesses genuinely quantum global features represents a great intellectual achievement, which so far has been carried out by means of human ingenuity.
Could this certification process be somehow automated? In this project, we exploit notions of artificial intelligence and condensed matter physics to devise algorithmic methods to detect global properties in many-body scenarios.
A inconvenient particularity of quantum many-body systems is that they cannot be fully comprehended in practice: since quantum mechanics requires exp[n] parameters to describe quantum systems of size n , carrying full state tomography, or even storing the full description of a quantum state in a computer memory, become infeasible operations. To tackle this obstacle, we propose two approaches:
Approach 1: don’t look at the whole, look at the pieces
While obtaining a whole description of a complex network (quantum or classical) is, in general, infeasible, fully characterizing a set of overlapping pieces thereof is a realistic task. Think of a 1-D many-body quantum system; one cannot characterize its overall quantum state, but one can obtain all its nearest-neighbors reduced density matrices with O(1) state preparations. If we had mathematical criteria to detect the desired physical property P given such marginal states, then we could provide a simple experimental protocol to certify P .

In this spirit, we studied how to characterize entanglement and nonlocality in translation-invariant infinite spin-chains from local measurements [1]. We found instances of TI quantum states with a nearest-neighbor state ρ1,2 that, despite being separable, allows one to conclude that the whole chain is entangled. We also solved the problem of determining whether a 1D translation-invariant box for infinitely many parties is nonlocal (see Beyond Quantum Theory), given the near-neighbor correlations. In the same line, in [2] we present a full, efficient characterization of the set of near-neighbor density matrices of fully separable quantum states in tree-like geometries. This includes a full characterization of n -partite correlators of fully separable TI states defined in the 1D infinite chain.
Our attempts to extend our results to higher spatial dimensions led us to tackle the classical marginal problem in 2D [3]. Consider an infinite square lattice, and suppose that each site gives one access to a unique random variable. A finite number of agents exploring this lattice would only have access to the random variables in their immediate surroundings. If this lattice happened to be translation-invariant, then the probability distributions of the variables probed by the agents would be constrained by this symmetry in a non-trivial way. The marginal problem consists in identifying all constraints which such marginal distributions are subject to, or, more poetically, to paint what these agents would see.
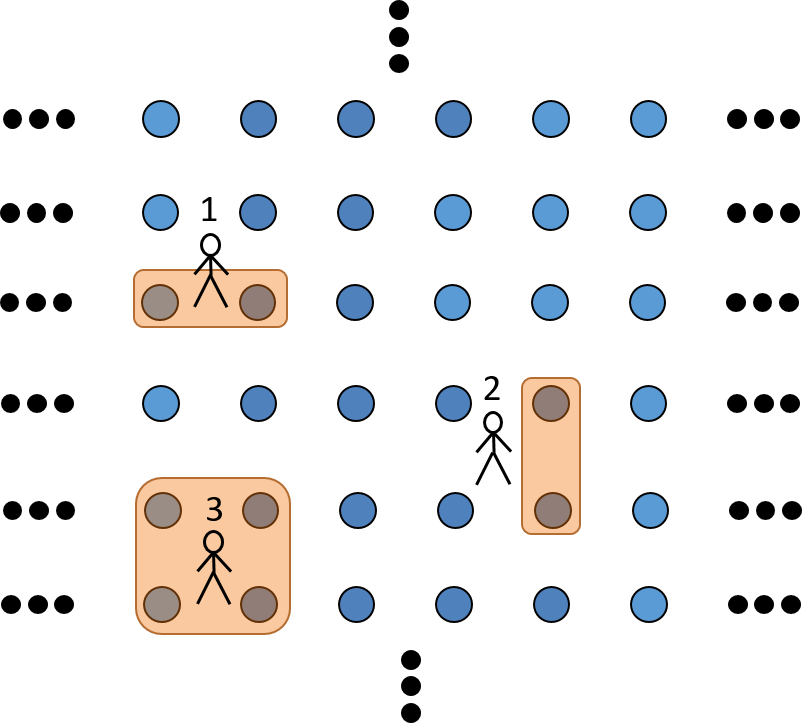
For instance, suppose that agents 1 and 2 in the Figure above estimate the probability distributions of the variables in one site and the site above (Pv(a,b) ) and one site and the site on its right (Ph(a,b) ). These distributions are so important in statistical physics that they have a name: they are called nearest-neighbor distributions. Given Ph, Pv , the marginal problem for nearest-neighbor distributions consists in determining whether there exists a 2D translation-invariant system with Ph, Pv as marginals. Similarly, we could have considered whether the 4-site distribution estimated by agent 3 is compatible with translation-invariance.
The marginal problem is solvable for 1D systems: given any distribution of a (finite) number of sites in a chain, there exists an algorithm with a fixed number of steps to decide if such a distribution could have arisen from a 1D translation-invariant system. It was by exploiting the solution of the 1D marginal problem that we managed to characterize nonlocality and entanglement in 1D quantum systems [2, 3]. In two spatial dimensions or more, the marginal problem was essentially unexplored. Hence we attacked it.
In [3] we find that the marginal problem in 2D can be solved for nearest-neighbor distributions when the random variables can just take d=3 possible values. It can also be solved for nearest-neighbor and next-to-nearest-neighbor distributions when d=2 . In such scenarios, it is possible to compute the minimum energy per site of arbitrary translation-invariant Hamiltonians analytically. In the latter, we can even calculate the number of lattice configurations achieving the minimum energy-per site.
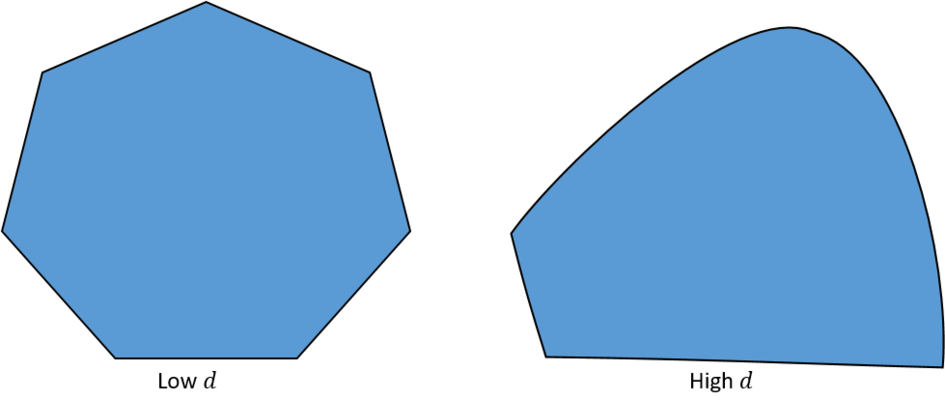
When viewed in probability space, the set of 2D TI marginal distributions in all solvable scenarios (including 1D) is a polytope, i.e., a set of points described by a finite number of linear inequalities, see the figure above, left. When d is of the order of thousands, the boundary of the set of nearest-neighbor marginals contains both flat and smoothly curved pieces, see the Figure above, right. Actually, for d=2947 , this set cannot even be described by a finite number of polynomial inequalities (namely, it is not semi-algebraic) [3]. To make matters worse, for arbitrary d , the minimum energy per site of a nearest-neighbor translation-invariant Hamiltonian is an incomputable function. That is, no Turing machine can evaluate it in all instances.
All the above makes exploring the entanglement and non-locality of 2D systems a challenging task.
Approach 2: only work with compressible networks
Most quantum networks are too complex to be fully comprehended. An obvious way to dodge this obstacle consists of studying only those networks that admit a computationally efficient description. As it turns out, the quantum state of many physical condensed matter systems can be (approximately) expressed through the contraction of a number of simple tensors. Such states are called tensor network states.
Deciding whether a quantum many-body state with a simple description has a specific global property is called the quantum information many-body problem, and, in [4], we propose a general method to tackle it. This method, connector theory, can be understood as a post-quantum extension of a fundamental tool in statistical physics: the quantum renormalization group.
To understand how connector theory works, think of the problem of deciding if a mutipartite box P, in the following to be represented by a black tensor, is Bell local. We first consider directed tensors of the form

with the property that, for all normalized Bell local boxes Q, the tensor

represents a sub-normalized Bell local box (mapping property). We call all such tensors connectors.
If we recursively apply coarse-graining connectors to the original box P, we end up with a smaller final box, whose non-locality can be established via some simple Bell inequality B (in turn, another connector).
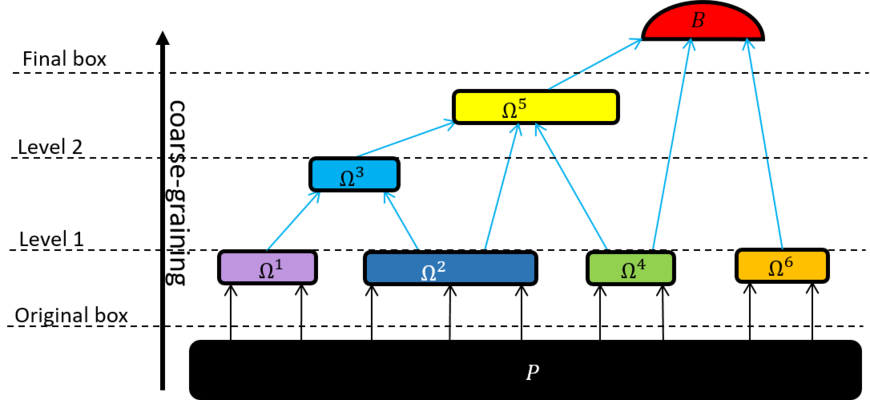
Due to the mapping property, if the final box happens to be detected by B, then P must be Bell nonlocal. Connectors thus relax complex nonlocality problems to much simpler ones.
In [4] we use techniques from machine learning to optimize over the connectors Ω1, Ω2 ,... so as to detect the non-locality of the original box P. If P happens to admit a matrix product state decomposition, the contraction between the connector tensor network and P can be computed in time linear on the system size (the number of parties in P). This observation allows us to detect non-locality in Bell scenarios with hundreds of parties.
For clarity, we just discussed the detection of Bell nonlocality through connector theory. However, there also exist connectors for quantum boxes or separable quantum states. Those objects, when contracted, respectively generate normalized quantum Bell inequalities and entanglement witnesses. See the paper for details!
[1] Z. Wang, S. Singh, M. Navascués, Entanglement and Nonlocality of 1D Macroscopic Systems, Phys. Rev. Lett. 118, 230401 (2017).
[2] Miguel Navascues, Flavio Baccari, Antonio Acin, Entanglement Marginal Problems, arXiv:2006.09064.
[3] Z. Wang and M. Navascués, Two Dimensional Translation-Invariant Probability Distributions: Approximations, Characterizations and No-Go Theorems, Proc. R. Soc. A 474: 20170822 (2018) .[
[4] M. Navascués, S. Singh and A. Acín, Connector Tensor Networks: A Renormalization-Type Approach to Quantum Certification, Phys. Rev. X 10, 021064 (2019).





