A notion of “classical'' temporal correlations correlations has been proposed by Leggett and Garg [1,2], based on the assumption of the existence of a definite value for physical properties at any time (realism) and the possibility of measurements that do not affect the subsequent evolution of such physical properties (noninvasive measurability). These classical models, called macrorealist admit bounds on the correlations observed in temporal sequences, the Leggett-Garg inequalities (LGI). Like Bell inequalities can disprove local hidden variable models, LGI can disprove macrorealist models when violated in an experiment.

The goal of Leggett and Garg was to investigate macroscopic quantum effects. The assumption of a noninvasive measurement is, in fact, justified by our everyday experience, but much less justified when dealing with microscopic systems. Similarly to Bell tests, where experimental loopholes are able to “save'' a local hidden variable description, logical weaknesses also arise in LGI tests: a violation of a LGI may be interpreted as the effect of a clumsy measurement that disturbs the systems (clumsiness loophole). 

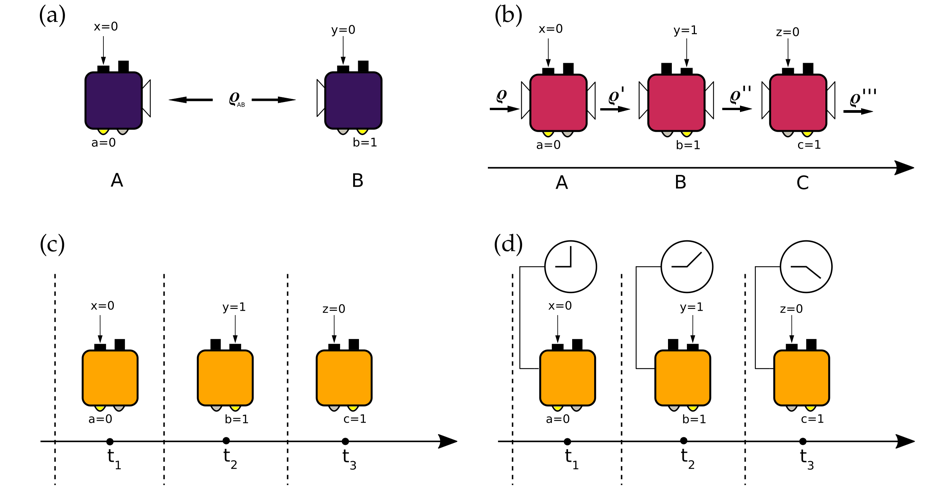
Fig .1 Graphical representation of possible measurement scenarios where quantum and
classical correlations can be compared. (a) Bell scenario. Two parties share a bipartite state ϱ_ABand perform measurements in two spacelike separated regions. (b) Communication cost scenario. Three parties perform measurements on a quantum system in a sequence, i.e., A performs a measurement and then sends the system to B, and so on.
(c) Memory cost scenario. The three boxes represent the same physical device at three instants of time. The box receives an input sequence (xyz) and generates an output sequence (abc). No external clock/memory is accessible to the box and hence its behavior is solely governed by its internal state. (d) Time-dependent operations. Same as before, but additional time information is provided by a clock, which allows the box to perform time-dependent operations. This scenario is equivalent to the one used for discussing communication cost in b

 

Is it possible to define a classical notion of temporal correlations without assuming noninvasive measurements? First, let us consider a box provided with an input sequence sin=(xyz) and that will produce an output sequence sout=(abc), with probability pout|in(abc|xyz) (see Fig.1). Due to the time ordering, all correlations can be decomposed as

pout|in(abc|xyz) = p(a|x)p(b|a;xy) p(c|ab;xyz)

where, e.g., p(c|ab;xyz) denotes the fact that the output c is a function of all previous inputs and outputs. Intuitively, all correlations can be generated if the system can store enough information of the previous inputs and outputs. In particular, this can be achieved by classical strategies.

This observation allows us to answer the above question in the negative: If no further constraints are imposed, classical systems are able to generate all time ordered correlations, hence, it is impossible to distinguish systems behaving according to classical, quantum, or more general probability theories. However, this also suggests a way of relaxing the assumption of noninvasive measurements to a weaker one: the system has a finite amount of memory. In this sense, we can see memory as the resource for generating temporal correlations. The case of noninvasive measurements, then, corresponds to a system not storing any memory and Leggett and Garg's notion of macrorealism is recovered as a special case.

Motivated by the above considerations, we investigate the structure of temporal correlations generated by systems with finite memory. In this framework, temporal inequalities can be obtained that distinguish between different theories (classical, quantum or general probabilistic theories) and systems of different dimension [3,4], minimal resources for the simulation of temporal correlations can be quantified [5], and  connected to practical applications such as the design of time-keeping devices (quantum clocks) [6].

 

 

[1] A. J. Leggett and A. Garg, “Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks?” Phys. Rev. Lett. 54, 857–860 (1985).

[2] C. Emary, N. Lambert, and F. Nori, “Leggett–Garg inequalities,” Rep. Prog.  Phys. 77, 016001 (2014).

[3] J. Hoffmann, C. Spee, O. Gühne, and C. Budroni, “Structure of temporal correlations of a qubit,” New J.  Phys. 20, 102001 (2018).

[4] C. Budroni, G. Fagundes, and M. Kleinmann, “Memory cost of temporal correlations,” New J.  Phys. 21, 093018 (2019).

[5] C. Spee, C. Budroni, and O. Gühne, “Simulating extremal temporal correlations,” New J.  Phys. 22, 103037 (2020).

[6] C. Budroni, G. Vitagliano, and M. P. Woods, “Nonclassical temporal correlations enhance the performance of ticking clocks,” arXiv (2020), arXiv:2005.04241 [quant-ph].

YIRG Group