Full experimental control over all relevant degrees of freedom is often not possible in real-world scenarios. There, an experimenter can manipulate only a certain set of degrees of freedom (the system of interest) that can be coupled to additional inaccessible degrees of freedom (the environment). For example, in quantum computation scenarios one has access to the respective qubit degrees of freedom, but those qubits interact in an uncontrollable way with their surroundings.  This coupling to additional, yet inaccessible, degrees of freedom allows for memory effects to travel not only through the system, but also through the environment. Such scenarios are studied in the field of open (quantum) system dynamics, and processes where the memory effects transported through the environment are non-negligible are called non-Markovian.

For such processes, one is interested in conditional probabilities for sequential measurements. It is natural to ask, how the size and type of the memory carrying environment influence and limit the observable joint probabilities pout|in(abc|xyz).

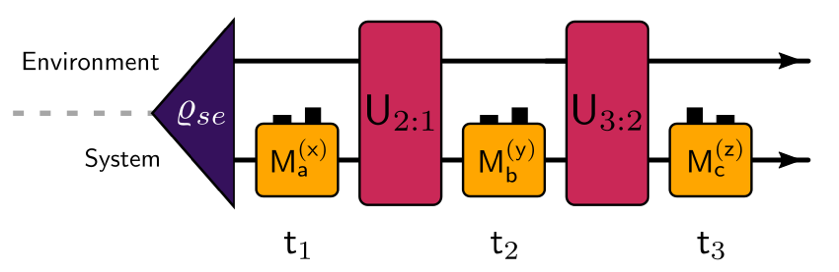
More concretely, in quantum mechanics, measurements are modeled by instruments, collections Ix  =  {Mi(x)} of completely positive maps that add up to a completely positive and trace preserving map. With this, conditional joint probabilities can be computed via

pout|in(abc|xyz)  =  tr[C(Ma(x) ⊗ Mb(y) ⊗ Mc(z))]    (2)

where the quantum combC contains all spatio-temporal correlations that can be observed. It is contingent on the initial system environment state as well as the coupling between the system (see Fig.1). Limiting either (or both) of these factors then restricts the set of observable correlations. With this in mind, we investigate the influence of quantum environments (as compared to classical ones) as well as the effect of dimensionality on observable correlations. 

 

 

Fig. 1 General dynamics (for three times) of a system coupled to an environment. (a) A controllable system of interest is coupled to an inaccessible environment. The former be probed by an experimenter at times t_1,t_2,t_3,.... In-between measurements, system and environment together undergo closed, i.e., unitary dynamics. (b) The action of all inaccessible parts of the dynamics can be combined into one single object, the quantum comb C depicted in blue (see Eq. (2)).

 

[1] P. Taranto, F. A. Pollock, S. Milz, M. Tomamichel, and K. Modi, “Quantum Markov Order”, Phys. Rev. Lett. 122, 140401 (2019).

[2] P. Taranto, S. Milz, F. A. Pollock, and K. Modi, “Structure of quantum stochastic processes with finite Markov order”, Phys. Rev. A 99, 042108 (2019)

[4] S. Milz, C. Spee, Z.-P. Xu, F. A. Pollock, K. Modi, and O. Gühne, “Genuine Multipartite Entanglement in Time”, arXiv:2011.09340 (2020).

[4] S. Milz and K. Modi, “Quantum stochastic processes and quantum non-Markovian phenomena”, arXiv:2012.01894 (2020)