Quantum Thermodynamics

Our research has contributed to the understanding of the foundations of thermodynamics in several ways: we have shown how thermalization can arise from quantum entanglement, we have proven that the non-equilibrium free energy has an exact operational interpretation for small systems without thermodynamic limit, and we have explored the fundamental limitations for the repeatable use of quantum resources.

Thermodynamics as a Resource Theory

In the last few years, quantum information theoretic ideas and methods have been used to study the foundations of thermodynamics from a completely new angle. Not only does this approach put thermodynamics on conceptually and mathematically rigorous grounds, but it also allows us to extend the laws of thermodynamics to regimes where the thermodynamic limit does not apply [5, 17, 18]: to small and strongly correlated (classical or quantum) systems.

This is achieved by reformulating thermodynamics as a Resource Theory: instead of analyzing how systems evolve in time (e.g. how gas molecules dynamically spread in a box), this approach views the laws of thermodynamics as consequences of an agent’s incomplete knowledge about (and control over) the physical system. For example, if we have a particle in a box, and we know whether a measurement would discover it in the left or the right half, we can insert a piston and extract work (as in a Szilard engine). On the other hand, if we don’t know, then trying to extract work will randomly lead to gain or loss. The agent's knowledge corresponds to a probability distribution or quantum state; the control restrictions (unitarity, exact preservation of energy) limit the processes that can be performed on the state, including work extraction processes.

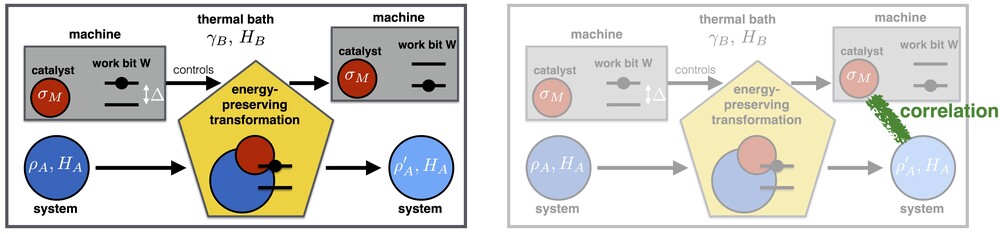
The process consists of a global unitary transformation U applied to the total system ABMW. Crucially, this transformation must exactly preserve the total energy (not just on average): we demand that [U, H_A+H_B+H_M+H_W]=0. In order to implement state transitions which cost work (or, similarly, yield some work gain), we allow the work bit to move from a pure excited state to its pure ground state (or vice versa).
Furthermore, we need our machine to remain intact, since we would like to apply it to other systems in the future. Its quantum state σ_M should  thus be exactly preserved in the process -- it should act as a catalyst. What is typically demanded in addition, however, is not only that the state of M remains exactly intact, but also that M remains uncorrelated with the system A.

Now, given any pair of initial and final states ρ_A and ρ'_A of A, under what conditions can the initial state be transformed into the desired final state by a "catalytic thermal operation" of this form? The authors of Ref. [18] have found necessary and sufficient conditions for this to be possible. Let us for the moment disregard the work bit (or, equivalently, set its energy gap to zero). Then, if the final state is blockdiagonal in energy, a transition is possible if and only if

F_α(ρ_A) ≥ F_α(ρ_A')   for all α≥0. 

The F_α denote a family of "free-energy-like" quantities. In the case of α=1, this is exactly the non-equilibrium free energy F=U-TS, with T the background temperature of the thermal bath. This family of inequalities is known as the "many second laws" of thermodynamics. It is no surprise that the usual second law (non-increase of F) becomes supplemented by additional constraints: after all, the standard second law is a statistical law that is valid in the thermodynamic limit, but here, we are considering transformations that are performed on single copies of a quantum system.

In Ref. [1], we have now considered a modified scenario that is depicted on the right-hand side of the figure above: it is exactly the same scenario as before, but now, we allow correlations to build up between the machine (catalyst) M and the system A. This leaves the machine intact, and allows it to perform similar state transitions on other systems (though not on exactly the same system again). In other words, this formalizes a weaker notion of "cyclicity". It can be shown that both notions of cyclicity (with or without correlations) agree in the standard textbook thermodynamic limit, but they turn out to differ significantly in the single-copy regime that we are considering here.

In fact, as we have proven in Ref. [1], allowing for correlations, a transition is now possible (for arbitrary blockdiagonal nonequilibrium states) if and only if

F(ρ_A) ≥ F(ρ'_A)

for the standard Helmholtz nonequilibrium free energy F=U-TS. In other words, this restores the validity of the "standard second law" in the regime of single-copy transformations. This is very surprising, because F and S=-tr(ρ log (ρ)) have been believed to attain their operational meaning only in the thermodynamic limit of many independent copies of a state.
Perhaps even more surprisingly, we have shown that the free-energy difference can be spent resp. extracted with an arbitrarily small amount of fluctuations (quasi-deterministically). Usually, fluctuations are "tamed" via the law of large numbers: for many copies of a state, quantities typically peak around their expectation values -- which is the basic phenomenon that allows us to derive "laws of thermodynamics" in the thermodynamic limit in the first place. Here, however, the fluctuations are in some sense "moved into the correlations", and almost-deterministic work extraction becomes possible.

No-broadcasting of coherence

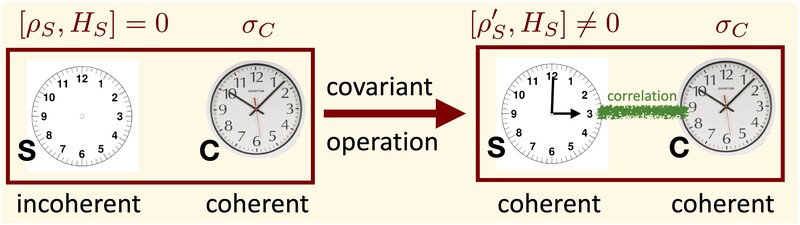
Above, we have only considered states that are block-diagonal in energy. But what about states that contain coherence between distinct energy levels? Can we have a catalyst that, for example, allows us to transform an incoherent state into a coherent one while exactly preserving its own (coherent) state?
In Ref. [6], we have proven that the answer to this question is negative: as long as the catalyst is finite-dimensional (which is arguably necessary to allow for full control of the corresponding state transition), such transitions are impossible. This result can also be interpreted in a different way: finite quantum clocks will necessarily have to degrade if their timing information is used on other quantum systems, even if the clock is used in a particularly clever way.
Such a forbidden broadcasting process is sketched in the picture below. The system C can be interpreted as a catalyst, or as a quantum clock. A very similar result has been proven independently and almost at the same time by Iman Marvian and Rob Spekkens [14].

Note, however, that a version of our result of Ref. [1] has recently been proven for quantum states with coherence in a remarkable paper [12]. Instead of considering thermal operations as depicted above, the authors consider the mathematically convenient, though perhaps physically slightly less physically motivated class of "Gibbs-preserving operations". They show that a correlated-catalytic Gibbs-preserving operation can induce a state transition if and only if F does not increase in the process, regardless of whether initial or final states contain coherence.
 

Von Neumann entropy from unitarity

Correlated catalysis is not only relevant in thermodynamics, but also in classical and quantum information theory. Here we have a similar phenomenon: Shannon entropy and von Neumann entropy S attain their operational meaning only in the limit of many copies of a given state. For example, Schumacher compression tells us that S gives the compression rate for quantum information sources in the limit of many identically and independently distributed instances of our quantum information source. On the other hand, for quantum information protocols that are not performed in this i.i.d. setting, typically so-called single-shot entropies (like min- and max-entropies) become the relevant quantities.

In Ref. [7], we have formulated -- and, in a special case, proven -- a conjecture on a single-copy operational interpretation of von Neumann entropy. This "Catalytic Entropy Conjecture" concerns again an arbitrary pair of quantum states, and the question whether the initial state can be transformed into the final state. In this case, the transition is demanded to be accomplished by a unitary operation. This unitary acts on the system A and another catalytic system B that is assumed to preserve its local state exactly.

In fact, in a follow-up work [13], Henrik Wilming from ETH Zurich has finally proven this conjecture. Thus, we now have an operational single-shot interpretation of the von Neumann entropy! This surprising and elegant insight raises the question of whether other standard entropic quantities (like the quantum relative entropy) can be given a "single-copy" operational interpretation.

Thermalization from entanglement

A complementary approach, also to a large extent motivated by quantum information, has been to take a dynamical point of view, and to ask: how do closed quantum systems thermalize? That is, why do “large” quantum systems seem to follow the predictions of thermodynamics, despite the fact that they evolve unitarily in time?

An exciting insight in the field has been that entanglement may play a crucial role here: if a quantum system is in a pure, but entangled state, then this means that it can be in a mixed state on a subsystem – and this mixed state can potentially resemble a statistical ensemble [15, 16]. This is impossible in classical physics, where maximal knowledge of the full system always implies maximal knowledge of all its parts.

This raises several questions: first, under what conditions do quantum systems equilibrate for (most) long times? For which systems is the equilibrium state independent from the initial state, and when is it actually identically to a thermal state, as predicted by textbook thermodynamics? In Ref. [8], we have shown (based on earlier mathematical physics results) that unitary evolution on a large class of translation-invariant quantum systems and initial states does in fact lead to thermal states (i.e. Gibbs states) on small subsystems.

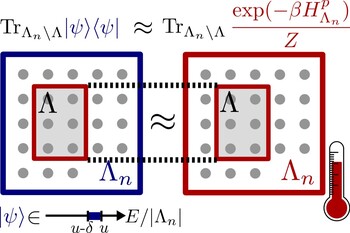
In another publication [9], we have proven that integrability does not play as important a role as it was widely believed before: there are non-integrable systems that nevertheless do not thermalize, in the sense that they keep some memory on their initial state. Furthermore, we have explored the Eigenstate Thermalization Hypothesis [19, 20], which claims that individual eigenstates on many-body systems typically resemble thermal states on subsystems. This hypothesis is still lacking a rigorous formulation and/or proof. In Ref. [11], we have found that a weak form of eigenstate thermalization holds in translation-invariant quasifree fermionic models. We have furthermore developed novel mathematical methods to prove concentration of measure for quantum states with a fixed expectation value [10], generalizing the notion of typicality to nonlinear sets of pure quantum states. To this end, we have combined methods of integral geometry with probabilistic tools and insights by Misha Gromov.