Certain theoretical proposals to solve the measurement problem in quantum mechanics postulate that closed quantum systems are subject to a non-unitary decohering process in the position basis. In principle, this non-thermal resource could be harnessed to extract work from nothingness via a suitable “collapse engine”, hence solving humanity’s long-standing energy problem. As put by the extra-terrestrial character Chocky in John Wyndham’s 1964 novel:
“[Your fuels] are your capital. When they are spent you will be back where you were before you found them. This is not progress, it is profligacy […]. Most of your power is being used to build machines to consume power faster and faster, while your sources of power remain finite. There can only be one end to that. You should be employing your resources, while you still have them, to tap and develop the use of a source of power which is not finite. Once you have access to an infinite supply of power you will have broken out of the closed circle of your solar-economy”. -John Wydnham, Chocky
Inspired by Wyndham’s prose, in [1] we hence tackle the general problem of how to incorporate a number of quantum channels into a thermal engine in order to distill a maximum amount of work. We manage to reduce the problem to a tractable optimization over finitely many variables, which we solve for the Ghirardi-Rhimini-Weber theory. We conclude that, under this model, collapse engines are indeed possible, but highly impractical: 1 kiloton of hydrogen is required to power a 40-Watt lightbulb indefinitely.
In the more than probable event that spontaneous collapse models are wrong and energy is locally conserved, the focus of human activities should be delaying the exhaustion of energy resources. In this line, in [2] we relate the maximum precision achievable in a quantum measurement with the average energy of the corresponding measurement apparatus.
In order to probe a quantum system, we make it interact with a measurement device, see the figure below. While in the classical case the role of the device or battery is merely to provide energy to the target system, in the quantum case, the measurement device also acts as a catalyst. By providing a resource of coherence between energy eigenstates, the measurement device is able to effect certain (otherwise impossible) evolutions on the system under observation.
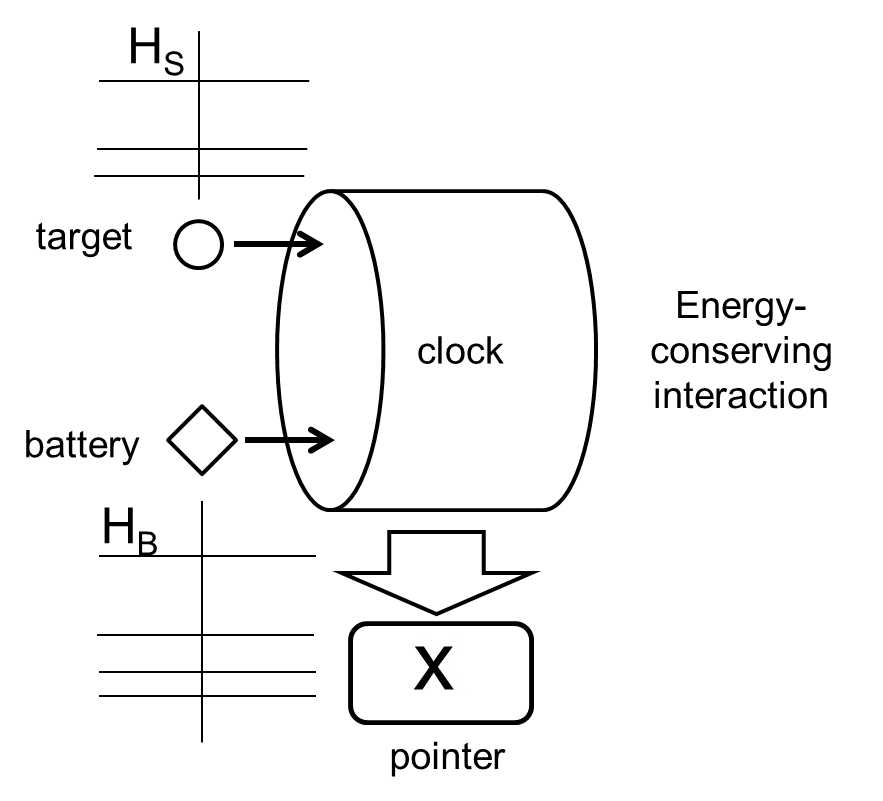
In [2], we study how constraints on the energy spectrum of a measurement device translate into limitations on the measurements that we can effect on a target system with a non-trivial energy operator. We find that certain measurements of two-level systems require an infinite amount of coherence (and thus, an infinite amount of energy) to be implemented. We also derive a universal relation between the average energy of a measurement device and the maximum precision of the measurements it allows to carry on two-level systems. More specifically, given a measurement device with average energy E used to probe a two-level system with energy gap ∆ , the inaccuracy ε of the device satisfies
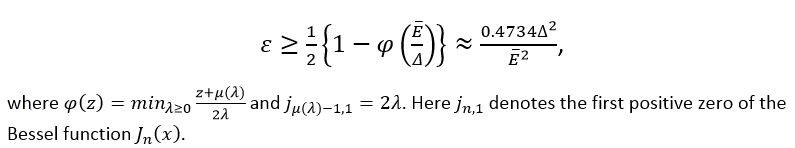
The measurement devices which saturate this relation are described by quantum states which have not appeared earlier in the literature. We call them battery states, and they perform substantially better than coherent states, the usual probe resource in quantum optics.
All the above applies only when the target is a two-level system. For higher dimensional targets, we devise algorithms to characterize the set of achievable measurements, given a promise on the energy spectrum of the probe, or its full state specification. Our work thus identifies the boundaries between what is possible or impossible to measure, i.e., between what we can see or not, when energy conservation is at stake.
[1] M. Navascués and L. P. García-Pintos, Non-thermal quantum channels as a thermodynamical resource, Phys. Rev. Lett. 115, 010405 (2015).
[2] M. Navascués and S. Popescu, How energy conservation limits our measurements, Phys. Rev. Lett. 112, 140502 (2014).




