The supposition that collective human behavior is guided by a set of equations and that one can use those to change the course of history through apparently harmless interventions is the basis of Isaac Asimov’s saga “Foundation”. It is of course, fiction, but, to which extend could it be true? Can we influence large, complex systems with the right manipulations? Is there such a thing as a foolproof plan? We explore these questions in three different scenarios: the research system, world pandemics and entanglement detection.

Research about research

For a theoretical physicist, applying for research funds is a long and unethical task. It involves concocting an elaborate fantasy where we pretend to know what we are going to discover in the next few years and how. This takes a lot of time away from research, around one month for the most important grants. Most importantly, it requires bullshitting in an official document.

We have reached this situation because, up to now, research policies have been based more on political fashion than on solid science. To progress beyond this point, we need an open scientific debate on research funding practices, where the scientific method is applied to the problem, i.e., with hypothesis, models, and experiments.

This is what we do in this paper [1]. We propose a research funding scheme by which each research unit (be it a single scientist, a group leader or a whole institute) applies for funding, but does not specify how much. The decision of how much funds (if any) must be awarded to each unit is taken by the funding agency, based on the recent scientific activity of the unit and the prior funding which such a unit was enjoying.

Of course, we work under the assumption that the agency has a clear notion of what it is about science that it wants to sponsor. There are many ways to quantify or evaluate scientific productivity, and deciding which one suits best reflects a political stance towards research. We personally advocate for evaluation methods based on peer-review rather than, e.g., bibliometric data. However, as we show in [1], once an agreed measure of scientific productivity is adopted, the distribution of research funds is no longer a political problem, but a mathematical one.

We start by modeling the research system as a collection of agents or research units, each of which possesses a “scientific productivity function”, indicating how much scientific production we can expect from a given research unit, when we hand it a given amount of funds for research. We allow productivity functions to be probabilistic and time-dependent. They are also secret, i.e., neither the research agency nor the scientists themselves know how they look like.

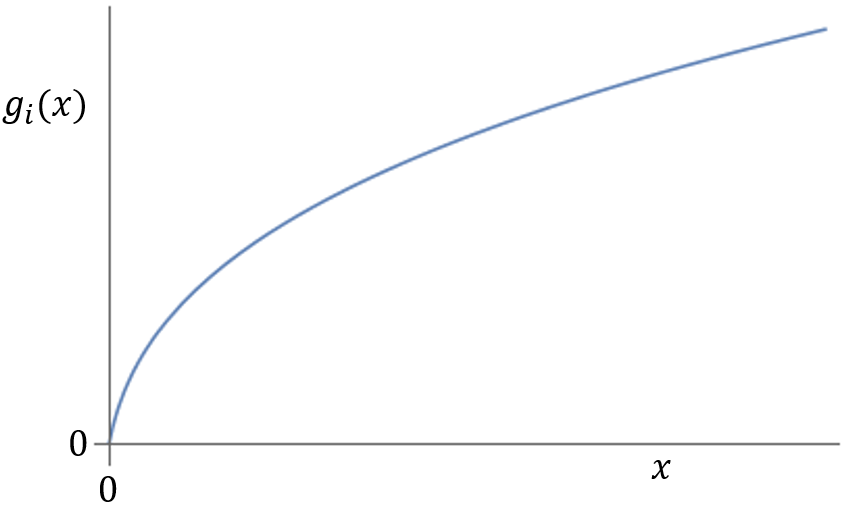
Scientific productivity of research unit i, as a function of the term funding x. It can be argued that this function (or its average value, if probabilistic) must be approximately increasing and concave.

Relying on our mathematical model of the research activity, we show that there exist systematic procedures to decide the budget distribution at each grant call with the property that the total productivity of the research community will be frequently not far off its optimal value.

The simplest of such procedures is what we call “the rule of three” (one could also call it "meritocracy"), by which the funds xk+1 for each research unit i at grant call k+1 are proportional to the research output gik of the unit during the kth term. If the total budget for science during the (k+1)th term is X euros, this means that

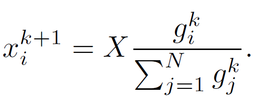
The rule-of-three quickly drives the research community towards a budget configuration that is independent of the initial funding conditions. Moreover, in the long run it guarantees at least half of the maximum scientific production achievable by the research system. Its returns must be compared with those of “excellence” schemes, whereby, under equal research outcomes, researchers which were funded in the past have a greater chance of receiving further funds. As we show, the latter policies very likely converge to configurations where the total scientific production is an arbitrarily small fraction of the maximum achievable by the research system. They are hence riskier than the rule of three.

In [1] we also study to what extent research policies can be cheated by dishonest research units. We conclude, for example, that hacks of the rule of three would require either influencing the evaluation stage or a coalition of research units.

In sum, what we propose is a radical reform of the current grant system. This reform is not a magical recipe for all the problems of scientific research. By itself, it won’t eliminate focus on popular topics, short-term goals, and conservative research. On the other hand, it won’t force theorists to engage in unethical practices, its funding decisions will be transparent and it won’t require the applicant to waste months of working time in writing project proposals. Moreover, we argue, using mathematical models, that it has the potential to steer the scientific community to a situation of maximal scientific productivity.

We hope that our work serves as the starting point for an academic (i.e., not political and definitely not administrative) debate on the way to manage publicly funded science.

Fighting diseases with mathematics

At the time of writing these lines, COVID-19 has caused nearly 5 million deaths worldwide. The government measures required to contain the disease in the year that followed COVID-19’s initial outbreak sunk the economies of many nations and provoked countless psychological issues on their citizenships. Some countries, like Nepal, endured a 120 days uninterrupted lockdown.

Most of the research on mathematical epidemiology focuses on modeling the free evolution of infectious diseases, or the effect of government interventions on the course of a pandemic. The problem of devising effective government policies for disease control is, however, grossly under-researched. Most schemes for disease control, such as pulsed vaccination, were discovered through a mixture of expert intuition and brute-force grid search. Policy generation is usually a two-step process: first, an expert epidemiologist proposes a family of strategies for disease control, depending on a small number of parameters; second, the effect of each of the strategies is simulated through mathematical models of disease spread; and third, the policy with the most suitable effects is recommended.

Despite its successes, this process is limited by the imagination and mental capacity of the human agents who conceive the policies. If the optimal policy of lockdowns and vaccinations required to contain a disease happens to be extremely complex, then it is unlikely to be discovered through this process.

In [2] we frame the task of finding suitable government policies for disease control as an optimization problem. In this problem, there is an objective function to be considered (e.g.: the total number of days under lockdown), together with a number of constraints (e.g.: that the number of occupied critical care beds does not exceed a threshold during the course of the government intervention). Our goal is to find the government policy that minimizes the objective function, while complying with the optimization constraints.

We find that one can adapt tools from machine learning and convex optimization theory to tackle disease control optimization problems with arbitrary constraints and objective function. The key idea is to realize that the gradient of the objective function with respect to the parameters describing the government intervention can be computed by solving a system of coupled differential equations. Very conveniently, this system has a complexity similar to that of the model used to describe the spread of the disease. In other words: as long as the government has enough computational resources to simulate the course of the pandemic, it can find the optimal intervention.

We applied our tools to identify a weekly policy of physical distancing measures that minimizes the associated economic burden, all the while keeping the occupation of critical care beds below the capacity in an imaginary country. The result is shown below.

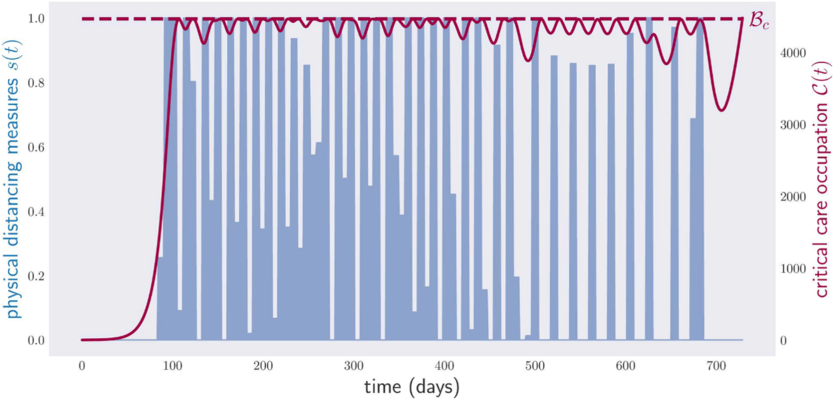
The generated policy is complicated to the point of practical infeasibility, but it illustrates a couple of ideas. First, our methods usually return optimal or quasi-optimal solutions; this follows from the fact that the critical care occupation repeatedly touches, but never surpasses, the country’s critical care capacity Bc . Second, objective functions must be chosen with care. Note that the slope of the critical care occupation curve is extremely acute near the end of the 2-year period optimized. The reason is that we asked the computer to find the policy with the smallest amount of social distancing measures for two years, and that is exactly what it did, in complete disregard of what happens afterwards.

We also considered how to adapt our techniques when the model depends on parameters that are not known with certainty. In that case, we postulate a probability distribution of model parameters λ  and the figure of merit is the statistical average of the objective function over λ . By recalculating a two-year lockdown policy plan every month or so, we adapt the policy to the growing knowledge of the disease dynamics.

Our work is nothing but the first step towards a full automation of policy generation. We still do not know how to take into account the mismatch between mathematical models and reality. That is, we lack efficient techniques to guarantee that a given policy will successfully contain the disease, even if the model to predict its evolution is not exact. But that is material for future research...

 

Quantum preparation games

Picture the following scenario: a quantum state is prepared and sent to a referee, who proceeds to measure it in some way depending on some internal variable called game configuration. Based on the measurement result, the referee modifies the game configuration. This process is iterated for a fixed number of rounds n . At the nth round, the referee assigns a score based on the final game configuration sn.

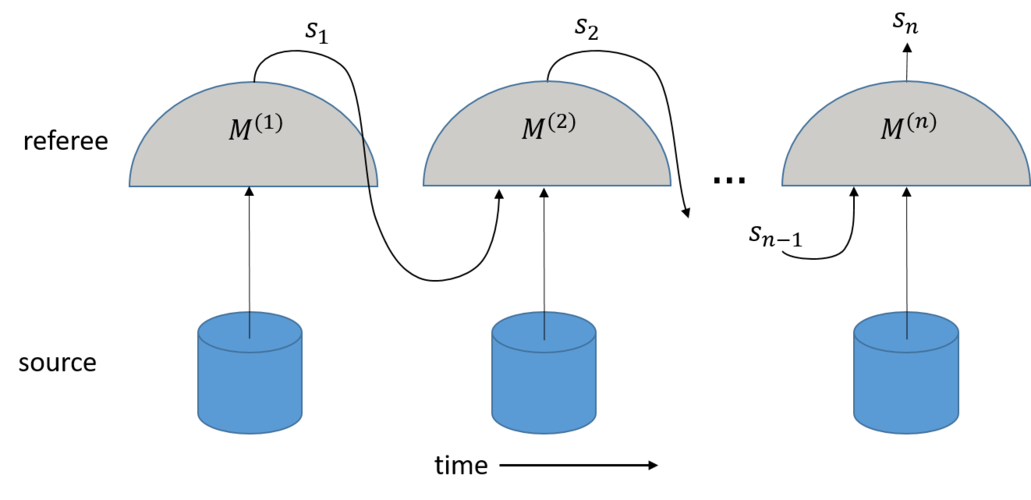
Sketch of a quantum preparation name. A source (the player) sends the referee a quantum state at each round. Depending on the current game configuration s, the referee probes the state and uses the measurement result to update the game configuration.

The primitive just described is a quantum preparation game. Many tasks in quantum information theory, such as Bell nonlocality demonstrations, entanglement quantification and magic state detection, can be formulated as a quantum preparation game. In [3] we introduce this notion and show how to compute the maximum average score of a given game when the player preparing the states is constrained to produce some subset of quantum states, e.g.: separable states. Note that, in each experimental round, the player is aware of the current game configuration, and might adapt its preparation correspondingly in order to increase its final average score. In other words, the player’s preparation strategy is adaptive.

In [3] we also explain how to devise non-trivial adaptive preparation games whose average score separates players with different constraints on their preparation devices. For a small number of rounds, we can even conduct full optimizations over quantum preparation games. Unfortunately, in the general case the number of game configurations scales exponentially with the number of rounds, so general optimizations over, say, 5 rounds become intractable. For n≈20 , one can however conduct approximate optimizations over quantum preparation games with a bounded number of game configurations via coordinate descent, i.e., optimizing the operations at each round.

To devise quantum preparation games for arbitrarily many rounds we introduce the notion of game composition. Suppose, for example, that our computational resources just allow us to optimize over 4-round preparation games. However, we wish to devise a 16-round preparation game. One way around this is to devise a 4-round meta-game, namely, a game in which, at each round, referee and player play a 4-round preparation game. Depending on the outcome of the game, the configuration of the meta-game changes and, based on it, in the next round the referee proposes a new 4-round preparation game. By recursion, one can define meta-meta preparation games, or meta-meta-meta preparation games. Curiously enough, we find that computing the average score of an n-round meta^j-game requires essentially the same resources as computing the average score of an n-round game. Moreover, when the meta-game consists of simply repeating the same dichotomic game several times and counting the number of victories, the best strategy available is proven to be playing the game optimally at each round.

 

[1] M. Navascués and C. Budroni, Theoretical research without projects, PLoS ONE 14(3): e0214026 (2019).

[2] M. Navascués, C. Budroni and Y. Guryanova, Disease control as an optimization problem, PLoS ONE 16(9): e0257958 (2021).

[3] M. Weilenmann, E. A. Aguilar and M. Navascués, Analysis and optimization of quantum adaptive measurement protocols with the framework of preparation games, Nat. Commun. 12, 4553 (2021).

Navascués Group