Large entangled quantum systems are required for many quantum information applications such as quantum computation or quantum communication. In addition, they form a perfect playground for fundamental questions of physics. These questions range from violations of local-realistic world-views to creating, controlling, and detecting entanglement in such complex systems.
Our small subgroup is mainly interested in finding new physical phenomena and concepts that allow experimental access to complex quantum systems. To do so, we develop and use the latest computer-based methods, such as Melvin [7] or online databases such as OEIS. The physical system in our case consists of single or multiple photons capable of encoding high-dimensional quantum information.

We investigate high-dimensional entanglement of photons encoded in transverse spatial modes – in particular modes carrying discrete quanta of orbital angular momentum (OAM). In contrast to the well-known property of polarization (which has two settings, thus can carry one bit of information), much more information can be encoded in the OAM of photons. We have shown that two photons can be entangled in more than 100 dimensions [1]. Furthermore, quantum entanglement with up to 10010ħ of angular momentum has been achieved in our labs, showing that systems with very large quanta can still possess the puzzling properties of the quantum world [2].

In parallel to increasing the dimensionality of the quantum systems, we also increase the complexity of those. We do so by simultaneously increasing the dimensions and the number of involved photons. In such systems, surprising new structures of asymmetric entanglement occur [3,4]. In addition, only very recently new types of violations of local realism have been found which can be applied to multi-particle high-dimensional quantum states [6]. Besides fundamental questions, they might lead to new ways for quantum communication [14] or quantum error correction.
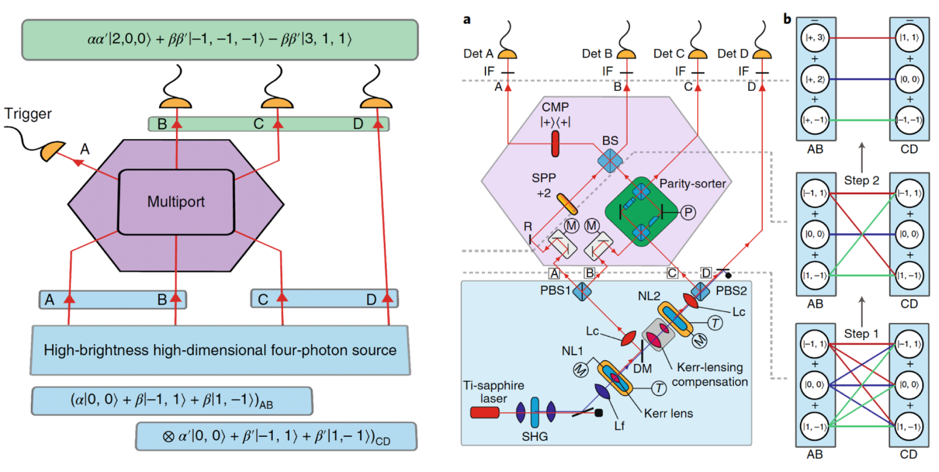
In our labs, we showed the first experimental realization of a multi-particle entangled state using the orbital angular momentum of light, where all photons are genuinely entangled in a high-dimensional manner [4]. Our experimental scheme employs a new type of multi-port (see Fig.3) that operates coherently and simultaneously on three photons in three dimensions each, forming a 27-dimensional operational space. In fact, the experimental generation of a three-dimensional GHZ state necessitates the manipulation of more than two photons in a higher-dimensional space.
The generation of complex high-dimensional quantum states is difficult in the laboratory. This is not only due to the strict technological requirements, but mostly because of the contra-intuitive quantum physical phenomena. Thus in many situations it is not even clear how to construct such quantum experiments. For that reason, we have developed a computer algorithm, which can propose new experimentally feasible setups [8,15,16].
Several of these computer-designed experiments have already been successfully implemented in our laboratories [3,4,8,16]. Recently, we showed that automated designs of quantum optical experiments by algorithms can not only produce specific quantum states or transformations, but can also be a source for inspiration for new techniques – which can further be investigated by human scientists in a broader context [9,11].
In line of this thought, we discovered a new technique called “Entanglement by Path Identity” [9]. This novel technique promises high brightness as well as scalable high-dimensional photon pair sources. It also enables the creation of multi-particle high-dimensionally entangled quantum states in a conceptually simple way.
Most interestingly, the use of Melvin in combination with the online encyclopedia of integer series (OEIS) led to the discovery of a previously unknown connection between graph-theory and quantum experiments [11,12,13]. This connection allows new insights into photonic quantum experiments and also revealed new ways for special purpose quantum computation [12].
Recent work:
Bibliography:
[1] Krenn, M., Huber, M., Fickler, R., Lapkiewicz, R., Ramelow, S., & Zeilinger, A. Generation and confirmation of a (100×100)-dimensional entangled quantum system. PNAS, 111(17), 6243-6247 (2014).
[2] Fickler, R., Campbell, G. T., Buchler, B. C., Lam, P. K., & Zeilinger, A. Quantum entanglement of angular momentum states with quantum numbers up to 10010. Proceedings of the National Academy of Sciences, 113(48), 13642-13647 (2016)
[3] Malik, M., Erhard, M., Huber, M., Krenn, M., Fickler, R., & Zeilinger, A. Multi-photon entanglement in high dimensions. Nature Photonics, 10(4), 248-252 (2016).
[4] Erhard, M., Malik, M., Krenn, M., & Zeilinger, A. Experimental Greenberger–Horne–Zeilinger entanglement beyond qubits. Nature Photonics, 12(12), 759 (2018).
[5] Huber, M., & de Vicente, J. I. Structure of multidimensional entanglement in multipartite systems. Physical review letters, 110(3), 030501 (2013).
[6] Lawrence, J. Rotational covariance and Greenberger-Horne-Zeilinger theorems for three or more particles of any dimension. Physical Review A, 89(1), 012105 (2014).
[7] Krenn, M., Malik, M., Fickler, R., Lapkiewicz, R., & Zeilinger, A. Automated search for new quantum experiments. Physical review letters, 116(9), 090405. (2016).
[8] Schlederer, F., Krenn, M., Fickler, R., Malik, M., & Zeilinger, A. Cyclic transformation of orbital angular momentum modes. New Journal of Physics, 18(4), 043019 (2016).
[9] Krenn, M., Hochrainer, A., Lahiri, M., & Zeilinger, A. Entanglement by Path Identity. Physical review letters, 118, 080401 (2017).
[10] Babazadeh, A., Erhard, M., Wang, F., Malik, M., Nouroozi, R., Krenn, M., & Zeilinger, A. High-dimensional single-photon quantum gates: Concepts and experiments. Physical review letters, 119(18), 180510. (2017)
[11] Krenn, M., Gu, X., & Zeilinger, A. Quantum experiments and graphs: Multiparty states as coherent superpositions of perfect matchings. Physical review letters, 119(24), 240403 (2017).
[12] Gu, X., Krenn, M., Erhard, M., & Zeilinger, A. Quantum Experiments and Graphs II: Computation and State Generation with Probabilistic Sources and Linear Optics. arXiv preprint arXiv:1803.10736. (2018)
[13] Gu, X., Chen, L., Zeilinger, A., & Krenn, M. Quantum Experiments and Graphs III: High-Dimensional and Multi-Particle Entanglement. arXiv preprint arXiv:1812.09558. (2018)
[14] Pivoluska, M., Huber, M., & Malik, M. Layered quantum key distribution. Physical Review A, 97(3), 032312 (2018).
[15] Gao, X., Krenn, M., Kysela, J., & Zeilinger, A. Arbitrary d-dimensional Pauli X-Gates of a flying Qudit. arXiv preprint arXiv:1811.01814 (2018).
[16] Gu, X., Krenn, M., Erhard, M., & Zeilinger, A. Gouy Phase Radial Mode Sorter for Light: Concepts and Experiments. Physical review letters, 120(10), 103601 (2018).