Cryptography is among the topics most affected by the development of quantum information theory. On one hand many popular cryptographic protocols are based on hardness of factoring and their security is seriously threatened by efficient quantum factoring algorithms. On the other hand, quantum mechanics provides tools to implement cryptographic primitives, such as quantum key distribution protocols or randomness expansion and amplification protocols [1] (for review also see [2]), which are inaccessible with classical resources only.
Quantum cryptography has become a thriving field with commercially available real world implementations. Existing quantum cryptographic protocols mostly employ qubits in two party scenarios. Nature, however, provides us with a much richer structure of quantum states, which are also potentially useful in various cryptographic scenarios. For example, we have studied quantum key distribution protocols based on high-dimensional bipartite entanglement and have shown that such a protocol is more resilient towards weak randomness attacks [3].
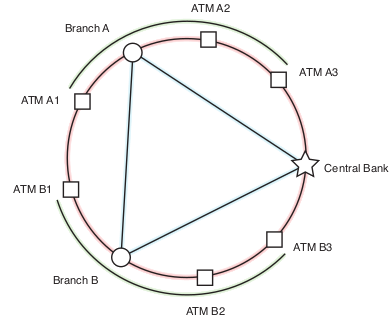
Moreover, multi-party high-dimensional entanglement is readily available in quantum photonics. Such states can be used as resources for novel multi-party cryptographic protocols. The simplest example is that of a quantum key distribution. In certain scenarios it is desirable that different subsets of N players need to share a secure key to use, for example, for secure broadcast. Thrillingly, multipartite high-dimensional entangled states can be used to create correlated data from which all these subset keys can be derived by classical post-processing, leading to a much more efficient protocol than running many copies of a bipartite protocol, achieving the same [4,5].
A central goal we are currently pursuing is finding more uses of high-dimensional multipartite states in quantum cryptography.
Recent work:
F. Brandt, M. Hiekkamäki, F. Bouchard, M. Huber, and R. Fickler, High-dimensional quantum gates using full-field spatial modes of photons. Optica, 7(2), 98-107 (2020).
[1] J. Bouda, M. Pawłowski, M. Pivoluska, M. Plesch, Device-independent randomness extraction from an arbitrarily weak min-entropy source, Phys. Rev. A 90, 032313 (2014).
[2] M. Pivoluska and M. Plesch, Device Independent Random Number Generation, Acta Physica Slovaca 64, No.6, 600 – 663 (2014).
[3] M. Huber and M. Pawłowski, Weak randomness in device-independent quantum key distribution and the advantage of using high-dimensional entanglement, Phys. Rev. A 88, 032309 (2013).
[4] M. Malik, M. Erhard, M. Huber, M. Krenn, R. Fickler, A. Zeilinger, Multi-photon entanglement in high dimensions, Nature Photonics 10, 248-252 (2016)
[5] M. Pivoluska, M. Huber, M. Malik, Layered Quantum Key Distribution, arXiv:1709.00377








