Quantum Metrology

Quantum metrology deals with questions regarding the precision with which unknown quantities can be estimated or detected. Utilizing the power of quantum mechanics advantages can be gained over previously known techniques for practical tasks such as parameter estimation, state discrimination, or hypothesis testing. In particular, non-classical effects can be harnessed to enhance the precision of determining quantities of interest such as magnetic fields, forces, phases, or frequencies. For many different applications, the quantum advantage manifests as a quadratic scaling gap in terms of the relevant resources, e.g., the number of sensing systems, with respect to the best classical approaches. For example, highly squeezed non-classical states may bring about a quadratic advantage when estimating certain Gaussian transformations [1].

 However, to achieve this so-called Heisenberg scaling, different tasks require different resource states as well as different (potentially non-local) measurements, which have to be separately determined for any specific case, rendering the design of a universally applicable, optimal sensing device difficult. Moreover, this still leaves open the important (and often ignored) question of how the desired states and measurements can be implemented efficiently. One research direction pursued in this group in collaboration with researchers in Innsbruck, Barcelona and Garching concerns the design of a flexible device that allows one to obtain a quantum scaling advantage for a large class of different metrological problems by using only a specific entangled state and single-qubit operations. As shown in [2], a 2D cluster state allows achieving Heisenberg scaling for an important group of paradigmatic metrology problems. This includes the sensing of local observables such as magnetic fields, as well as the estimation of phases, frequencies, and certain interaction strengths. Crucially, we show that this can be done both in the local (frequentist) approach with arbitrarily many repetitions, and in the (single-shot) Bayesian approach for arbitrary cost functions and priors.

The optimal probe state for these different problems vary strongly, ranging from Greenberger-Horne-Zeilinger (GHZ) states in the case of local phase estimation, to certain superpositions of states with different Hamming weights for Bayesian phase estimation. Moreover, also the corresponding optimal measurements are vastly different, including simple local measurements for GHZ states, but also complicated, entangled measurements on all qubits, e.g., discrete Fourier basis measurements for Bayesian estimation. In particular, some states and measurements may be significantly more difficult to realize than others. The 2D cluster state allows one to deal with all of these problems. On the one hand, the fact that it is a universal resource for measurement-based quantum computation (MBQC) trivially enables arbitrary state preparation and measurements on a subset of the qubits in the cluster, provided the latter is large enough. On the other hand, MBQC provides a simple, unifying framework in which state preparation and measurements can be assigned an unambiguous resource cost in terms of the overall number of qubits in the cluster, as illustrated in Fig. 1.

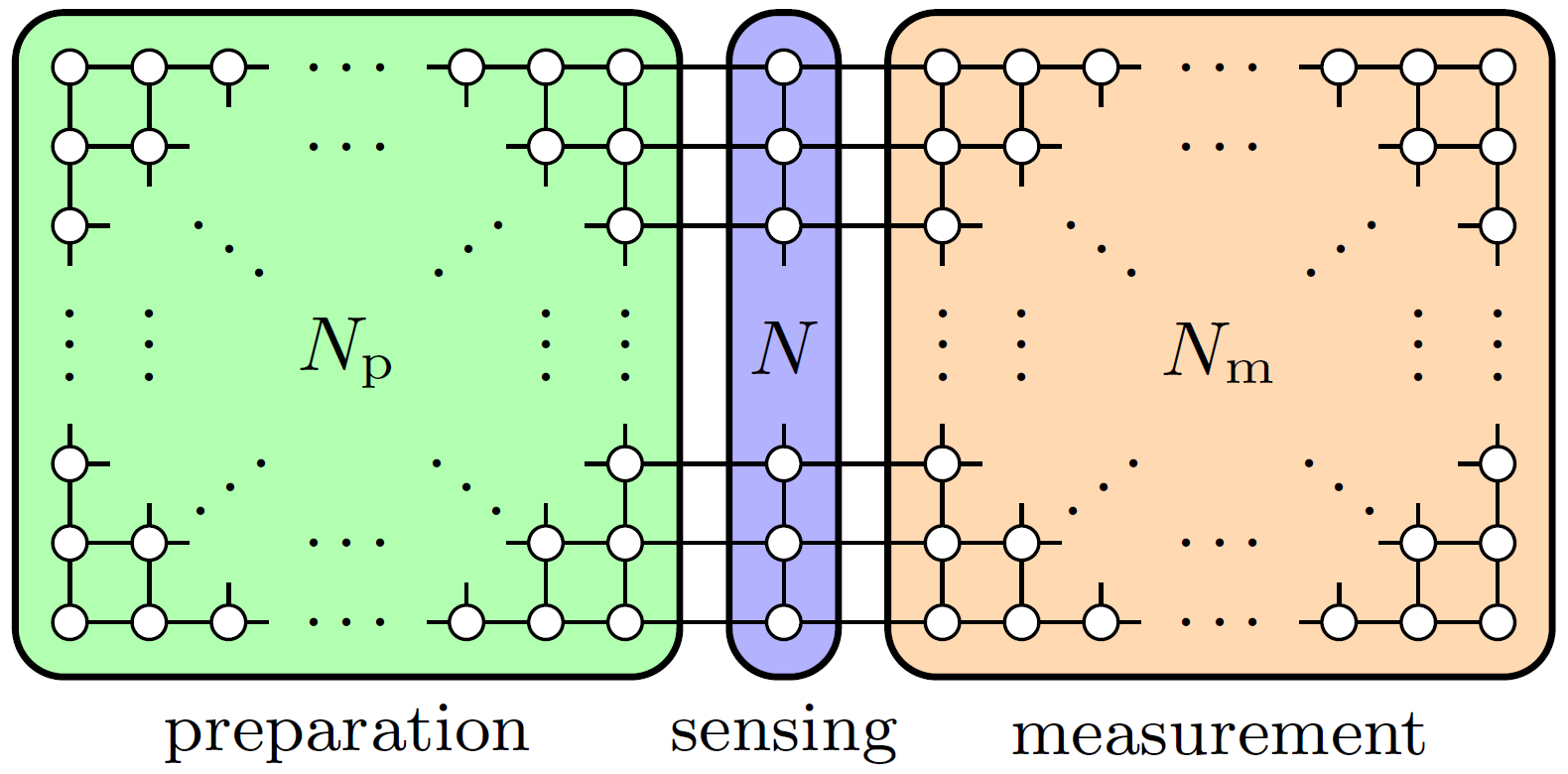
To guarantee a quantum scaling advantage for metrological applications, the probe preparation and measurements must be efficiently executable. That is, any metrological scaling advantage is lost if the size of the cluster required for a given estimation strategy with an N-qubit probe grows as N² or stronger, in which case it becomes favourable to use all qubits in the cluster as individual, classical probes instead. We show that the preparation of optimal probe states and corresponding suitable measurements for local as well as Bayesian phase and frequency estimation can indeed be carried out efficiently using 2D cluster states. For the local scenario, we explicitly construct the preparation and measurement strategy achieving optimality. For the Bayesian scenario, we present a construction that can generate all optimal probe states with a linear overhead in N. We then introduce a compression procedure that can be implemented on a 2D cluster with O(N log2N) qubits, which enables one to efficiently perform measurements even when the circuit descriptions of the corresponding unitaries are of exponential size in the number of qubits of the compressed space. These constructions allow achieving Heisenberg scaling for phase and frequency estimation scenarios using the 2D cluster in a flexible manner. Crucially, this flexibility holds the potential for yielding (nearly) optimal scaling performance for a variety of estimation problems, and hence goes beyond the capabilities of architectures dedicated to specific individual tasks.

[1] N. Friis, M. Skotiniotis, I. Fuentes, and W. Dür, Heisenberg scaling in Gaussian quantum metrology, Phys. Rev. A 92, 022106 (2015) [arXiv:1502.07654].

[2] N. Friis, D. Orsucci, M. Skotiniotis, P. Sekatski, V. Dunjko, H. J. Briegel, and W. Dür, Flexible resources for quantum metrology, New J. Phys. 19, 063044 (2017) [arXiv:1610.09999].