Full Network Nonlocality

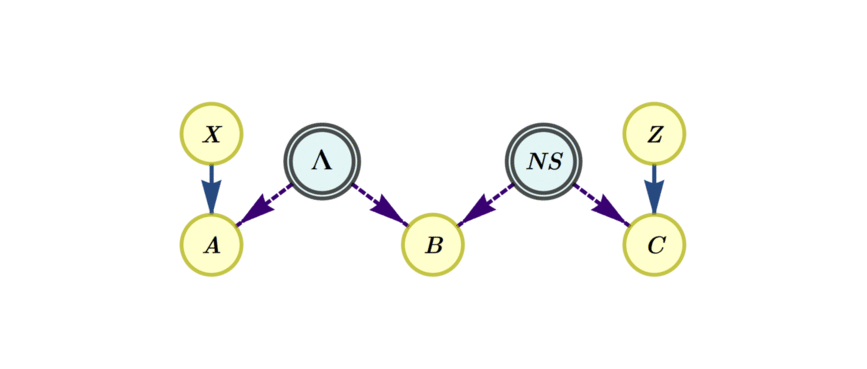
Figure 1. Three-party entanglement swapping network. The left source is described by local hidden variables and the right source is a general nonlocal box.

 Quantum networks are under rapid development. This has motivated a research program aiming to understand the types of quantum information protocols that they may support. This endeavor also carries substantial foundational interest: networksare an invitation to go beyond the traditional scenarios in which quantum theory is commonly investigated and explore potentially novel forms of nonclassical features of the theory. In general, a network is a structure in which a number of parties are connected to each other through a set of independent sources. The most famous classical analog is the internet – whose quantum version is one of the major goals of the field. The simplest quantum example is the entanglement-swapping scenario, in which two sources connect three parties pairwise (see figure).

Network nonlocality is, however, both a technically and conceptually challenging enterprise. The former is due to the fact the main tools developed for Bell nonlocality over recent decades do not apply to networks. The latter is due to the difficulty of pinpointing what truly constitutes a network phenomenon, as opposed to standard Bell nonlocality. At the origin of this lays the fact that the very definition of locality in a network is the subject of debate. Naturally generalizing Bell’s local causality assumption, a network phenomenon is said to be local if it can be understood exclusively in terms of local hidden variables. Although this is many times the desirable definition, it also has multiple drawbacks. Most conspicuously, two parties on the fringe of the network who violate a standard Bell inequality will cause the entire network statistics to be labeled as nonlocal. This is just Bell’s theorem disguised as a network phenomenon. Concerns in this spirit have for years called for stronger notions of network locality that capture various interesting aspect of network phenomena.

The present article puts forward the first attempt at proposing a stronger, more genuine, definition of network locality. The main idea is simple: the statistics produced in a network is proposed to be fully network nonlocal if it necessitates that every source is a nonlocal resource. In other words, if there exists a model in which one source in the network is described by local hidden variables and all other sources are (perhaps post-quantum) nonlocal resources, then the statistics are still viewed as network local. This idea can be thought of as nonlocality everywhere.

Full network nonlocality demands considerable revision of standard network Bell tests. It is found that the most famous network Bell inequality cannot detect full network nonlocality in quantum theory. A model in which one source has a local hidden variable description (Figure, left source) and the other source has a general nonlocal description (Figure, right source) is sufficient to simulate every quantum violation.  This means that the several experiments recently conducted in this scenario are insufficient to reveal this stronger notion of network nonlocality. In fact, it turns out that also the experiments that consider more sophisticated network scenarios also fail to reveal full network nonlocality – either due to fundamental reasons (as in the scenario of the Figure) or due to insufficient quality in the experimentally reported Bell parameters. In the article, both general methods and concrete tests are developed to detect full network nonlocality and it is shown that quantum theory can pass these tests even with presently available technology. In this sense, full network nonlocality paves the way for a new series of more convincing network nonlocality experiments as well as lays the first stone in the endeavor to systematically understand what genuine quantum phenomena in networks may look like.